こんにちは、マイクです。

前回の記事で出したクイズの答は考えましたか？

おさらいをすると、下のチャートで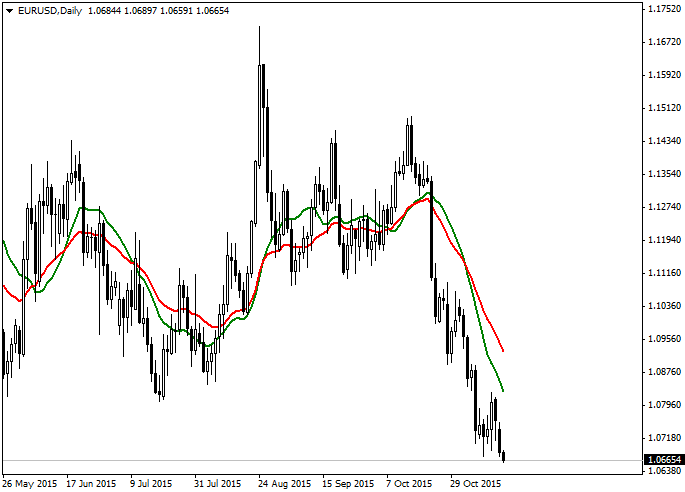


2本の移動平均線のうち、どちらがSMAで、どちらがEMAでしょうか？

というクイズでした。


さて、正解は：

• 緑がSMA、赤がEMA

です。


あれっ？？

EMAの方がSMAよりもローソクに近くなるはずだから、反対じゃないの？？

と思った方、いらっしゃいますか？


「EMAの方がSMAよりもローソクに近くなる」ということが言えるのは、両者の期間が等しい時です。

実は、上のチャートのSMAとEMAは期間が違います。

SMAが15期間、EMAが25期間になっているのです。


ちなみに、両方とも期間を20に揃えると、下のようになります：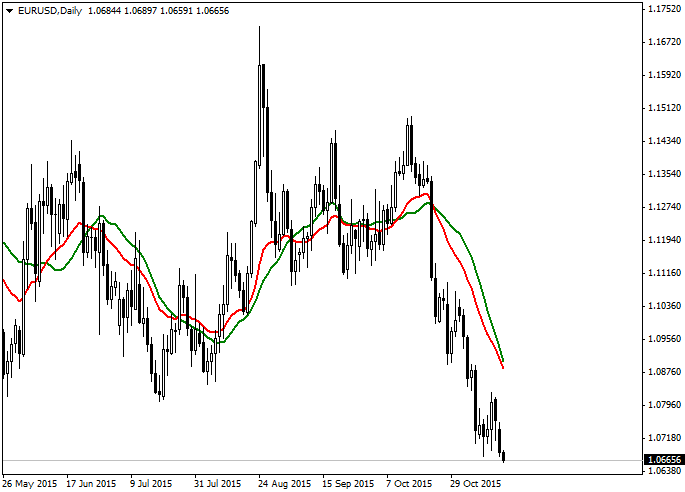



これだとイメージ通りではないでしょうか。

つまり、ローソクに近いかどうかは期間の長さが強く影響し、必ずしもEMAとSMAの特性の違いを表すものではないということがわかります。


では、ここで、MAの「期間」について改めて考えてみましょう。

時刻\(t\)での期間\(n\)のSMAは次式で定義されます：

\[\mathrm{SMA}(t)=\frac{1}{n}\sum_{j=0}^{n-1}p(t-j)\tag{1}\]

但し、\(p(t)\)は時刻\(t\)のローソクの終値です。

単純に現在から過去\(n\)本のローソクの終値の平均を取ったものですね。


一方、EMAは次式で定義されます：

\[\mathrm{EMA}(t)=\alpha\sum_{j=0}^{\infty}(1-\alpha)^j p(t-j)\tag{2}\]

ここで、

\[\alpha=\frac{2}{n+1}\]


式(2)を見るとわかりますが、EMAの場合には平均を求めるのに使われるデータが理論上無限に過去を遡ります。


では、EMAにおける「期間」\(n\)は、いったい何を表しているのでしょうか？


次回までにみなさんも考えてみてください♪


では、今日もポチっと応援お願いします☆

↓↓↓↓↓↓