こんにちは、マイクです。

前回の記事では、SMAとEMAの定義を示し、期間\(n\)のSMAは過去\(n\)本の終値から計算されるのに対し、EMAは理論上無限大の本数の過去データを使わないと求められないことがわかりました。

ここで疑問となるのが、

EMAの「期間」にはいったい何の意味があるのか？

ということです。


それを理解するためには、EMAが過去のデータに対し、どのような「重み」を付けて平均を取っているのかを見てみる必要があります。

下の図をご覧ください：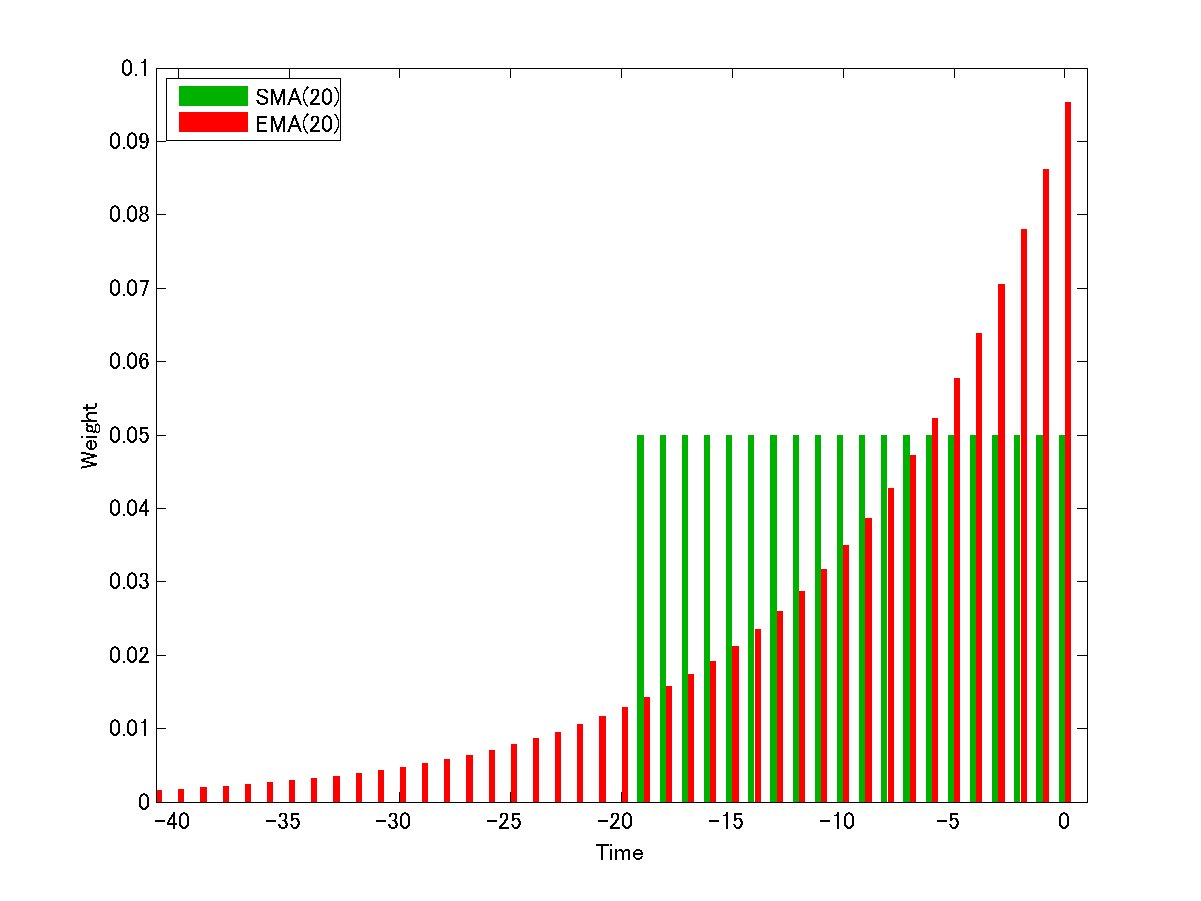

現在の時刻を0としたとき、期間\(n\)=20のSMAとEMAで、それぞれ過去\(j\)番目のデータにどれだけの重みが掛かっているかを示したものです。

SMAの重みは

\[{}_sw_j=\left\{\begin{array}{cl}\displaystyle\frac{1}{n}&\quad(0\le j < n)\\0&\quad(j \ge n)\end{array}\right.\]

なので、20本は全て等しく0.05となり、それより過去は0です。


一方、EMAの重みは

\[{}_ew_j=\alpha (1-\alpha)^j\]

なので、現在のバーの重みが

\[{}_ew_0=\alpha=\frac{2}{n+1}=0.0952\]

20本目の重みは

\[{}_ew_{19}=\alpha(1-\alpha)^{19}=0.0142\]

となり、SMAの重みと比べると、それぞれ2倍弱・1/4強となります。


この「2倍弱・1/4強」という関係は、\(n\)がある程度以上の大きさの場合だいたい同じで、\(n\rightarrow \infty\)の極限では、それぞれ2と\(2e^{-2}\)=0.2707に収束します。


つまり、EMAの「期間」とは、同期間のSMAと比べた時に重みがだいたいこのぐらいの関係になるという「目安」だと考えればよいということになります。


では、この重みの分布形状の差異がもたらすSMAとEMAとの最も特徴的な違いは何でしょうか？


これも次回までに考えてみてください♪


では、今日もポチっと応援お願いします☆

↓↓↓↓↓↓