こんにちは、マイクです。
前回の記事で「鳥肌立ちました。。」発言を紹介させて頂いた友達が、早速その記事にコメントを入れてくれました♪
こういう反応を頂けるのはほんとに嬉しいことですね。![]()
ありがとうございます!
さて、今日は遅行スパンとローソク足との乖離が大きい時を見てみましょう♪
前回までの記事はこちらから:
■「マイクの定理」とその応用(1)
■「マイクの定理」とその応用(2)
■「マイクの定理」とその応用(3)
■「マイクの定理」とその応用(4)
■「マイクの定理」とその応用(5)
下のチャートをご覧ください。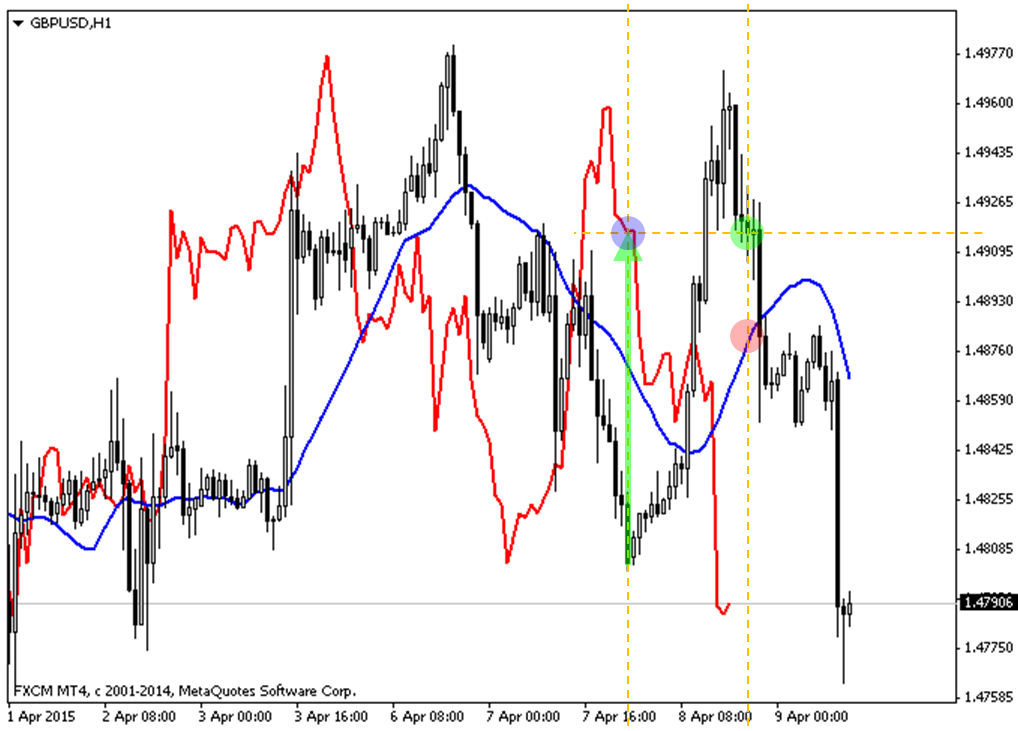
緑の矢印で示したのが、直近の上昇時に遅行スパンとローソク足が最も乖離したところです。
その時の遅行スパン(青○)に対応する時刻のローソク足は緑○で示しています。
そして、その時刻のMAを見てください(赤○)。
ここでMAは最も急な上昇角を付けています。
遅行スパンとローソク足との乖離が最大になると同時に、MAの角度も最大になったということですね。
MAの角度が最大ということは、上昇の勢いがピークであることを示しています。
遅行スパンとローソク足の乖離がトレンドの勢いを示していることと見事に呼応していますね!
ここでも「マイクの定理」がそれを理論的に説明していることになります♪
さて次回は、遅行スパンとローソク足が絡み合う場面を見てみましょう。
では、今日もポチっと☆

はじめまして、マイクさん
遅行スパンの解説、見事です。
遅行スパンの威力は、すごいと思っていたのですが、その理由が分からないでいました。腑に落ちました。ありがとうございます。
自分の場合は、遅行スパンとほとんど同じですが、移動線を後ろにではなく、前に移動させた、先行移動線を使っています。過去検証するなら、先行移動線の方が、分かり易いと個人的には思います。
ウーゴさん、こんにちは。
応援ありがとうございます♪
確かに過去検証では、注目するローソク足に対応する遅行スパンがどこなのか、わかりにくいですよね。
その点、先行移動線の場合には、注目するローソク足自体が遅行スパンの役割を担うので、視線が彷徨わず(笑)、確かにわかりやすいと思います!
読者のみなさんにも参考になると思います。
シェアして頂き、ありがとうございました。
今後ともよろしくお願いいたします。