こんにちは、マイクです。
前回の続きですので、まだ記事を読んでいない方はこちらから:
■「マイクの定理」とその応用(1)
■「マイクの定理」とその応用(2)
早速、式(2)に移ります。
\[A_n(t)=n(\mu_n(t)-\mu_n(t-1))\tag{2}\]
「角度」とは「傾き」と言い換えられます。
つまり、\(n\)期間単純移動平均線\(\mu_n\)の時刻\(t\)における角度\(A_n(t)\)とは、下の図で言うと、\[A_n(t)=\frac{\Delta y}{\Delta x}\]ですね(青い線がMA)。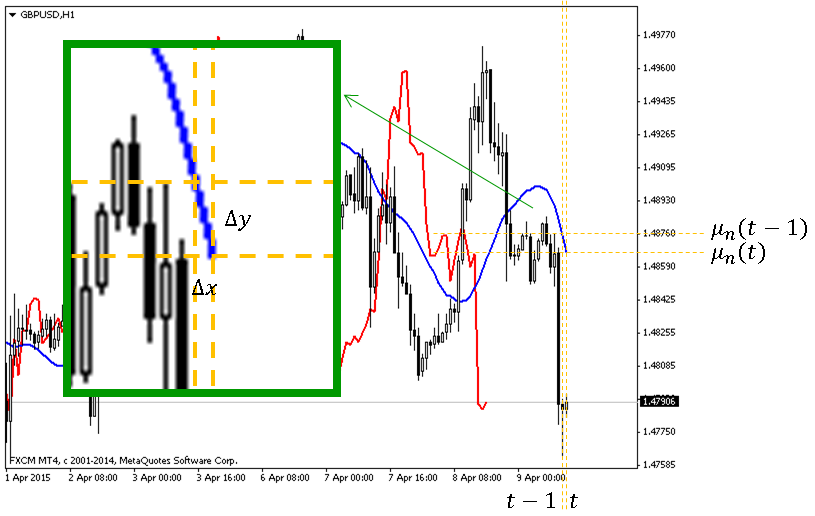
ここで、\(\Delta y=\mu_n(t)-\mu_n(t-1)\)です。
そして、横軸方向の間隔は期間\(n\)で基準化されるので、\(\Delta x=1/n\)となります。
よって、MAの角度は\[A_n(t)=n(\mu_n(t)-\mu_n(t-1))\]で表されることがわかりました。![]()
次回は、いよいよ式(3)を証明しましょうね♪
では、今日もポチっと☆

マイクさん
新ブログ開設、おめでうございます!
知識の宝箱!
頑張って勉強させてもらいます♪
早速、ロット計算機、使わせてもらいましたっ!
すごーーーーく便利、
もう、手放せないデス♪♪
とっちーさん、こんばんは!
ロット計算機、気に入ってくれて嬉しいです。
いつもお供にしてやってください♪
ブログ記事も更に濃くなりますので、どうぞお楽しみに!
マイクさん ご栄転おめでとうございます(笑)
前のブログも見られるようにしてくださってありがとうございます^^
仲間で検証してる時 ここはマイクさんの三種の神器だよね~とようやく見つけられるようになった美穂は大喜びしています。少しづつ 少しづつでも日々成長です^^
今回のブログもまた学びがいっぱいなんだろうな~楽しみです。
(*゚▽゚*)
美穂さん、こんにちは!
「ご栄転」って!?笑
「三種の神器」はいろんなところに隠れてますからね♪
見つけ出してかわいがってやってください。笑
継続は最強の力、楽しく勉強していきましょう♪