こんにちは、マイクです。

前回の記事では、1年間分の1時間足6201データの解析を通して、

「ボリンジャーバンドの各バンド内に値動きが収まる確率は、±1σ内が68.27%、±2σ内が95.45%、±3σ内が99.73%」

という都市伝説が誤りであること実証しました。

あ、これまでの記事を読んでいない方はこちらからどうぞ：

■ボリンジャーの都市伝説(1)
■ボリンジャーの都市伝説(2)

で、そもそも「都市伝説」のパーセンテージ、

• ±1σ内：68.27%
• ±2σ内：95.45%
• ±3σ内：99.73%

という数字は、何を根拠に出てきたものなのか？

という話になったのでした。


実は、これらの数字は確率統計をかじったことがある方にはお馴染みの数字ですね。


それは、正規分布に従う確率変数が、期待値\(\pm n\)標準偏差(\(n=1, 2, 3\))内の値を取る確率\(P(n)\)です。

その値は、標準正規確率密度関数

\[f(x)=\frac{1}{\sqrt{2\pi}}\exp \left( -\frac{x^2}{2} \right)\]

を用いて、

\[P(n)=\int_{-n}^n f(x) dx\]

で求めることができます。


要するに、都市伝説の誤りは、本来、正規分布とはかけ離れた分布形状をしているものに、正規分布を特徴づけるパーセンテージを当てはめてしまったことに起因するのがわかります。


では、いったいどのくらい違う分布なのか比べて見てみましょう。

下の図を見てください：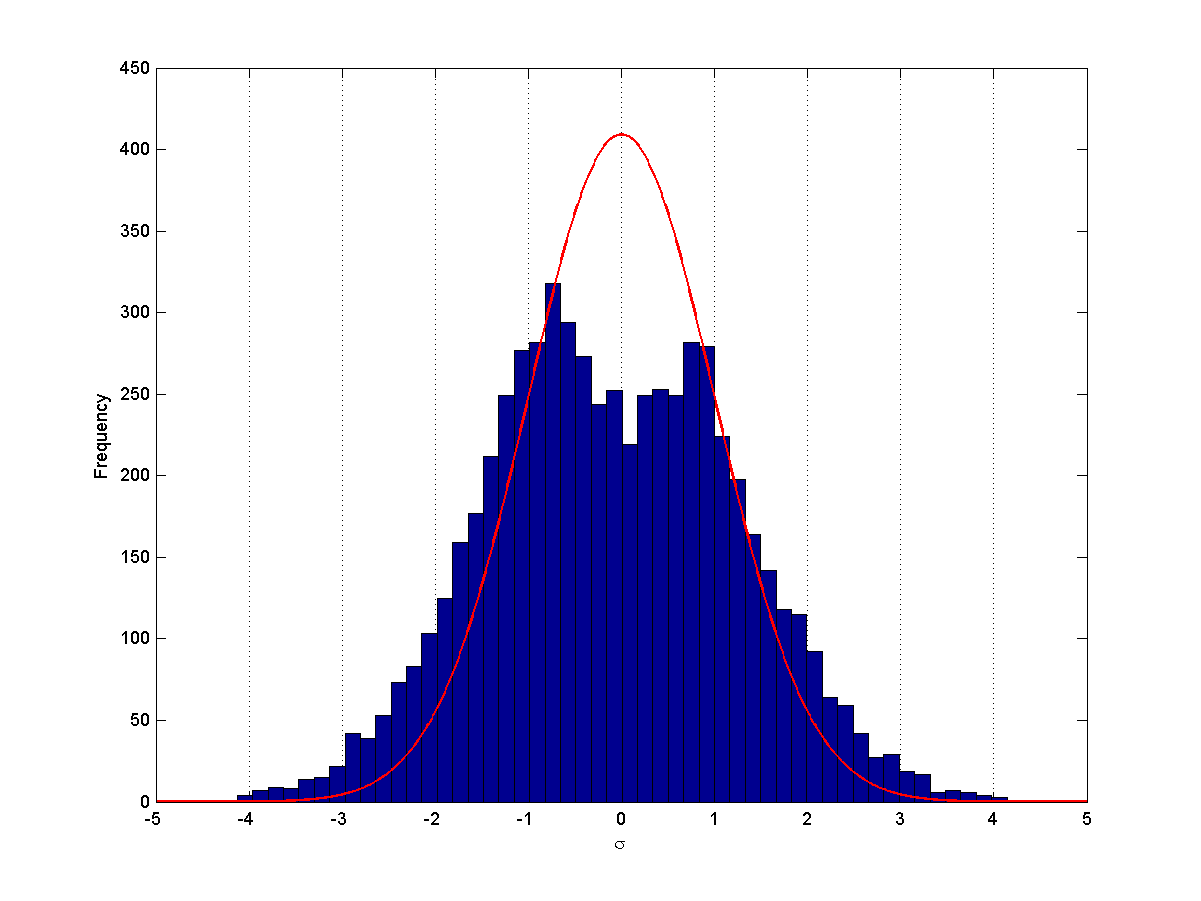


前回の頻度分布に、標準正規分布の確率密度関数を赤い線で重ねてみました。

縦軸は、積分した面積が等しくなるようにスケーリングしています。


これを見ると違いが一目瞭然ですね！

正規分布はツンとしたきれいな山の形状ですが、ボリンジャーバンドにおける価格分布は、頂部が叩き潰されたように凹んでいます。

それで、±1σ内のパーセンテージにあれだけ大きな差がでたわけですね。


そして、ボリンジャーバンドにおける価格分布は、正規分布に比べて裾野が遠くまで広がっていることがわかります。

正規分布は±3σではほぼ0に近いですが、ボリンジャーバンドにおける価格分布はもっと遠くまではみ出していますね。

だから価格が±3σを外れることも、実際にはざらにあるわけです。


それにしても、ボリンジャーバンドにおける価格分布が0付近で谷を形成していることは意味深です。

これは価格がMAの近傍には滞留しにくいことを示唆しているからです。

この点については、また機会を改めて論ずることにしましょう。


ところで、都市伝説は、このような分布形状の違いを無視しているばかりか、確率論的に非常に重要な特徴量である標準偏差の解釈についても勘違いをしています。


？？？


それについてはまた次回お話ししましょう♪


では、今日もポチっと応援お願いします☆
↓↓↓↓↓↓