こんにちは、マイクです。

前回の記事では、

「ボリンジャーバンドの各バンド内に値動きが収まる確率は、±1σ内が68.27%、±2σ内が95.45%、±3σ内が99.73%」

という都市伝説が発生した原因が、

「本来、正規分布とはかけ離れた分布形状をしているものに、正規分布を特徴づけるパーセンテージを当てはめてしまった」

ことであるのが判明しました。


これまでの記事を読んでいない方はこちらからどうぞ：

■ボリンジャーの都市伝説(1)
■ボリンジャーの都市伝説(2)
■ボリンジャーの都市伝説(3)


で、実は、その分布形状の違いを無視していることの他に、都市伝説は、確率論的に非常に重要な特徴量である標準偏差の解釈についても勘違いをしていると指摘しましたが、これはどういうことでしょうか？


そもそもボリンジャーバンドとは、過去一定期間の終値から、その標本平均と標本標準偏差を求めたものです。

一方、都市伝説は、その標本平均を原点、その標本標準偏差をスケールとした、値動きの相対位置の分布について言及しています。


・・・ん？？？


なんかおかしい！


と思いませんか？


そうです。


都市伝説は、その相対位置の分布自体の標準偏差が、スケールの単位に等しい、つまり、1であることを、暗黙の裡に仮定しています。

もちろんこれには何の根拠もありません。

同じ「標準偏差」という名前から混同したのでしょうね。


では、実際には値動きの相対位置の分布の標準偏差はどのくらいなのでしょうか？


これまで例として取り上げている1年間分の1時間足6201データに対して算出したところ、

\[\sigma=1.34\]

となりました。


都市伝説の暗黙の仮定よりも、35%も大きいですね。


分布形状の違い以前の問題とも言えます。


前回のグラフにこの幅を重ね描いたのが下の図です：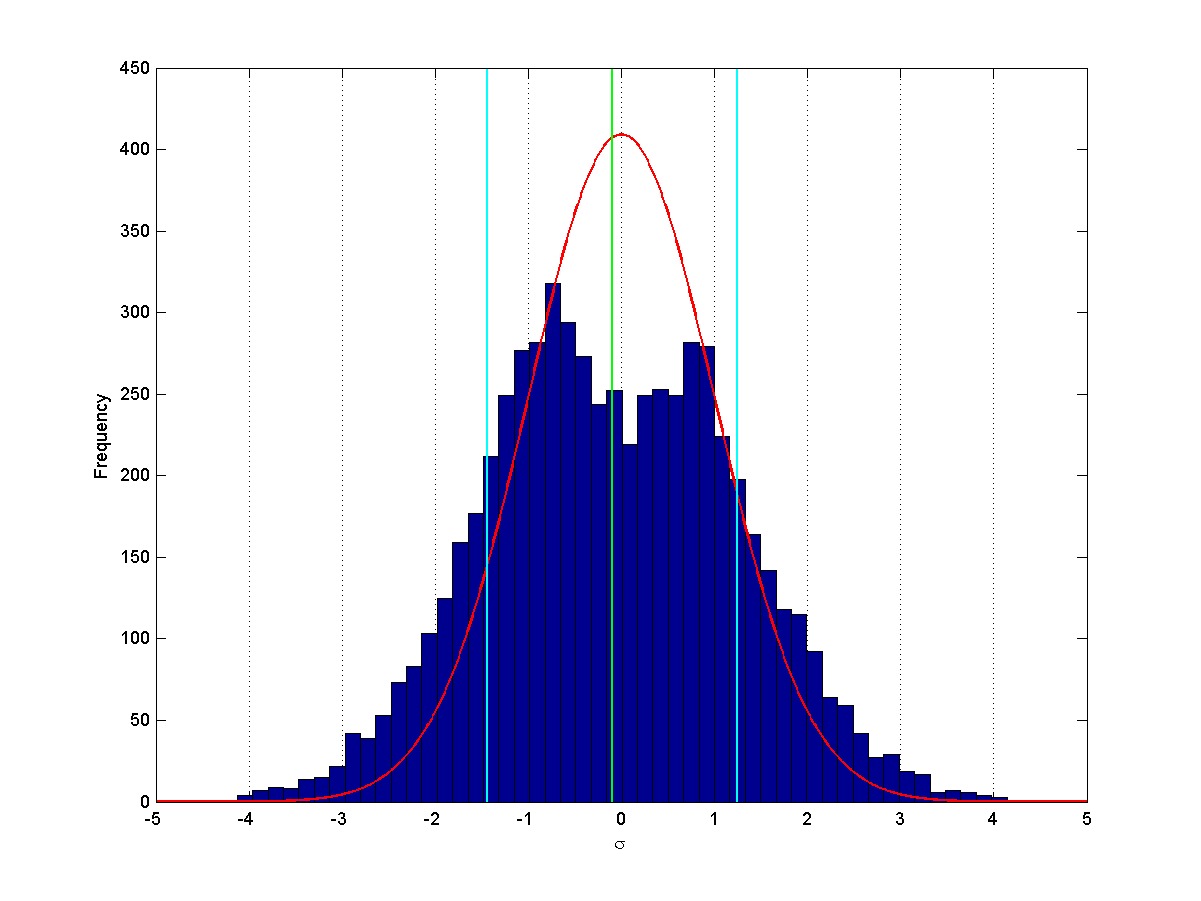


緑の線が分布の平均、水色の線が±1σです。

BB±1σとこれだけ幅が違います。

こうなるともう、何を比較しているかわからないですね。爆


結局、都市伝説は、

• 分布形状の違いを無視
• 標準偏差の意味を混同

という二重の誤謬を犯していることがわかりました。


あー、すっきりした♪


では、今日もポチっと応援お願いします☆
↓↓↓↓↓↓