こんにちは、マイクです。

前回の記事では、価格 \(p\) が時間 \(t\) に比例して上昇しているケースで、

• 価格変動はフラクタルか？
• もしそうであれば、次元はいくつか？

というクイズを出しました。

みなさん、考えましたか？

この答を出すには、下のようなグラフを描いてみるといいですね：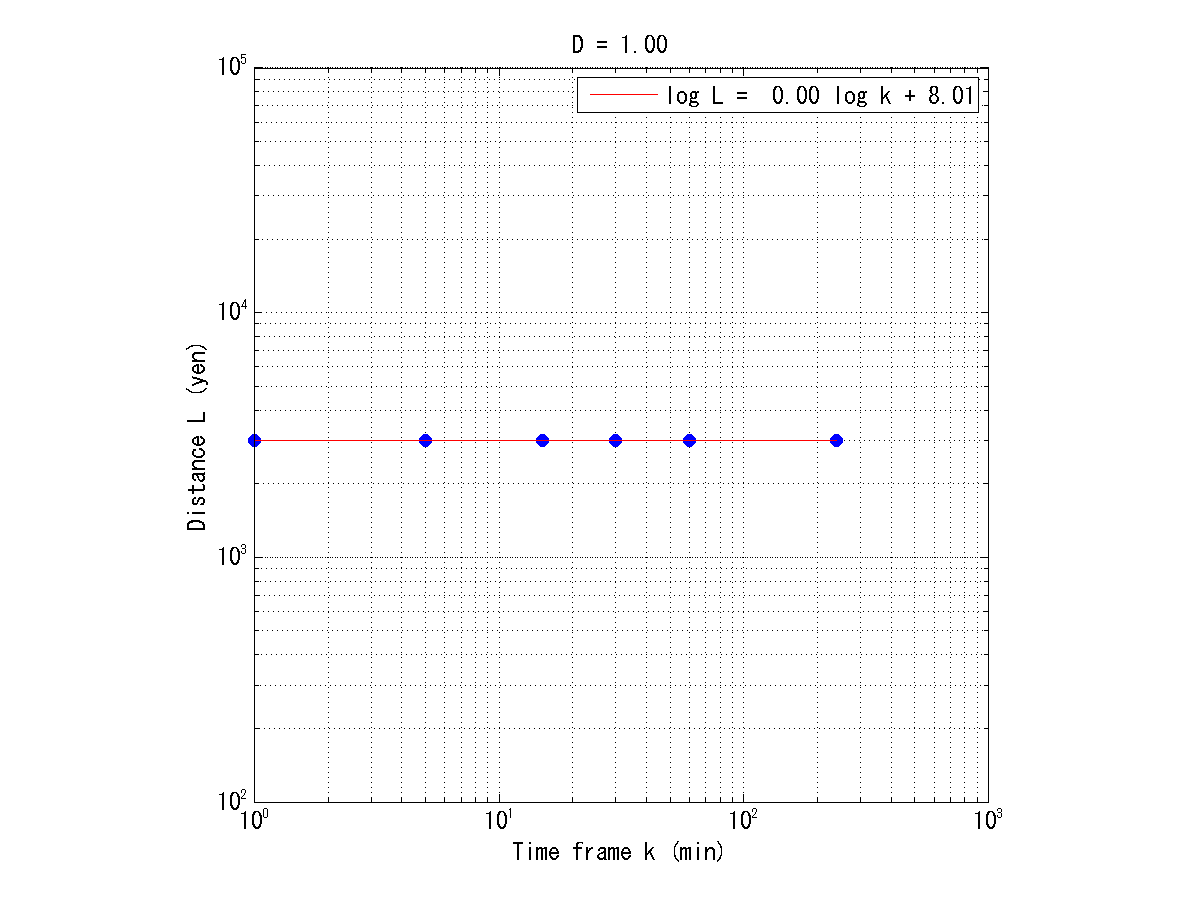


横軸は粗視化のスケール(つまり時間足) \(k\)、縦軸は各スケールに対応する距離で、両方とも対数軸になっています。

プロットしている点は、1分足、5分足、15分足、30分足、1時間足、4時間足にあたります。

前回の記事でも指摘した通り、このケースでは、粗視化スケールによらず距離は一定となるので、プロットは水平線上に並びます。


ということは・・・


まず、データセットがフラクタルであるためには、対数軸上でプロットが直線上にあることが必要でしたね。

ということは、その条件については満たされています。

よって、このデータセットは「フラクタルである」と言えます。


次に、そのフラクタル次元を求めます。

この場合、直線の傾きは「0」ですから、

\[1-D=0\]

となり、フラクタル次元は、\(D=1\) となります。


ん・・・？


それって・・・？


もともとのスカラーの1次元と同じじゃん！


そうなんです。爆


このケースは、定義から言うと確かにフラクタルです。

実際、一部分を拡大しても全体と同じ形をしているので、自己相似性も有しています。

しかし、フラクタル特有の「複雑性」が皆無ですね。笑

これはあまりに自明、言わば、「トリビアルなフラクタル」と呼べるでしょう。


こんな例を持ち出したのは、フラクタル性の判別の仕方とフラクタル次元の求め方を、わかりやすく説明するためです。


次回は、いよいよ実際のチャートデータを用いてフラクタル解析を行います！

どうぞお楽しみに♪


では、今日もポチっと応援お願いします☆

↓↓↓↓↓↓