こんにちは、マイクです。

いつも応援ありがとうございます♪
↓↓↓↓↓↓ 



前回の記事では、プライスの到達点を到達点を推し量るために使われるインジケータである、

Fibonacci Expansion (FE)

と

マイナスのフィボ

について比較し、両者のラインに不思議な合致が見られる場合があることを、実際のチャートを例に解説しました。

具体的には、リトレースがちょうどFib 38.2%の深さになっている場合、

・FE 061.8%　＝　Fib -023.6%
・FE 100.0%　＝　Fib -061.8%
・FE 161.8%　＝　Fib -123.6%

というラインの合致が起こっていたのでした。


この意味をよりよく理解するために、FEとFibのみを表示した図を示します：

■リトレース：Fib 38.2%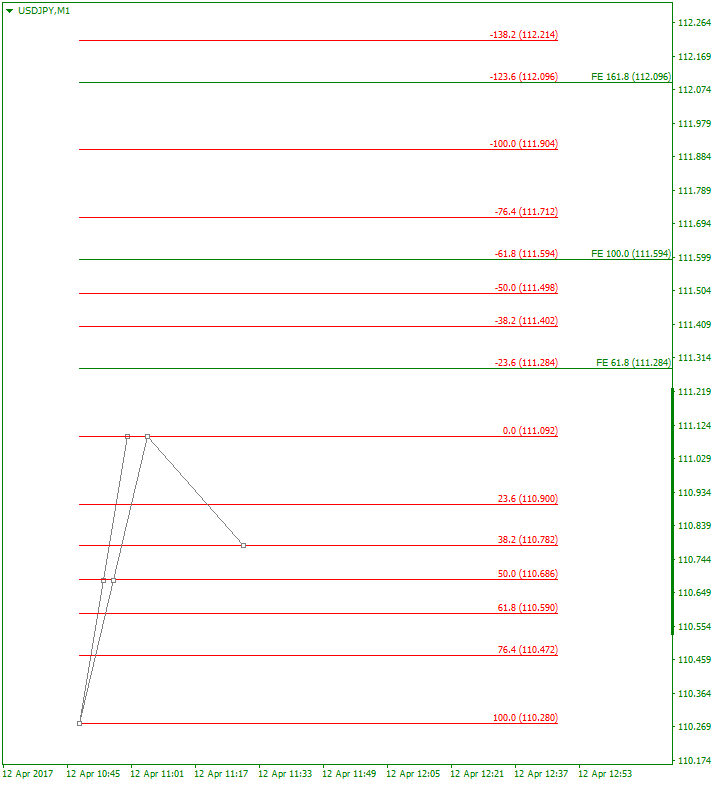


そもそもFibもFEも、

黄金比

に基づいて作成されたスケールです。

黄金比\(\phi\)は、フラクタル(自己相似)性を有する黄金長方形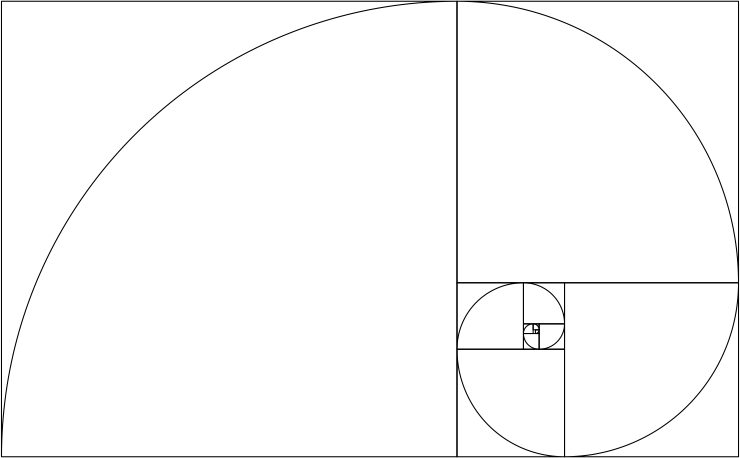


の短辺に対する長辺の比です。

つまり、
\[\frac{1}{\phi}=\phi-1\tag{1}\]
の解ですね。

これを解くと、
\[\phi=\frac{1\pm\sqrt{5}}{2}\]
ですが、
\[\phi>0\]
なので、結局
\[\phi=\frac{1+\sqrt{5}}{2}\approx 1.618\tag{2}\]
となります。

はい、FEでお馴染みの161.8%こそが、他ならぬ黄金比なのでした。


ここでもう一度式(1)を見てみましょう。

この式を日本語にすると、

「黄金比の逆数は黄金比から1を引いたものと等しい」

ですね。

つまり、黄金比の逆数を\(\lambda\)とおけば、
\[\lambda=\frac{1}{\phi}=\phi-1\approx 0.618\tag{3}\]
となります。

おー、またFibでお馴染みの61.8%が出てきました！

これは黄金比の逆数だったのですね。

さて、再び式(1)を\(\lambda\)で書き直すと、
\[\lambda=\frac{1}{\lambda}-1\]
となります。

これを変形すると、
\[\lambda^2=1-\lambda\approx 0.382\tag{4}\]
となり、ここで38.2%が出てきました。

更に両辺に\(\lambda\)を掛けると、
\[\lambda^3=\lambda-\lambda^2\approx 0.236\tag{5}\]
となり、23.6%も導かれます。

更に\(\lambda\)を掛けていくとどうなるかは、以前の記事に書きましたので参照してください。


ここで改めてFEの各レベルについて考えてみると、リトレースした3点目からFibのマイナス方向に、それぞれ

・FE 061.8：\(\lambda\)
・FE 100.0：\(1\)
・FE 161.8：\(\phi\)

だけ動くということです。

よって、今回の例のようにリトレースが38.2%\(=\lambda^2\)の場合、FEの各レベルをFibに換算すると、

・FE 061.8% \(=\lambda^2-\lambda=-\lambda^3\approx-0.236\)
・FE 100.0% \(=\lambda^2-1=-\lambda\approx-0.618\)
・FE 161.8% \(=\lambda^2-\phi=-(1+\lambda^3)\approx-1.236\)

となり、マイナスのフィボの各レベルに対応することがわかりました！

やはり黄金比は神秘的ですね♪


では次回は、リトレースの深さが異なる場合の対応関係について見てみましょう。

どうぞお楽しみに♪


では、ポチっと応援お願いします☆

↓↓↓↓↓↓