こんにちは、マイクです。
いつも応援ありがとうございます♪
↓↓↓↓↓↓
![]()
前回の記事では、FEとフィボが共に「黄金比」に基づいてフラクタルに構成されているが故に生ずる両者のラインの合致について、リトレースの深さが38.2%の場合の対応関係を解説しました。
これまでの記事はこちらから:
■Fibonacci Expansionとマイナスのフィボ(その1:不思議な合致)
■Fibonacci Expansionとマイナスのフィボ(その2:黄金比が導く対応関係)
■Fibonacci Expansionとマイナスのフィボ(その1:不思議な合致)
■Fibonacci Expansionとマイナスのフィボ(その2:黄金比が導く対応関係)
今回は、リトレースの深さが異なる場合に、その対応関係がどのように変化するのかを見てみましょう。
前回示したケースも含めて、リトレースの深さが下記の3通りの場合について調べます:
■ 23.6% \(=\lambda^3\)
■ 38.2% \(=\lambda^2\)
■ 61.8% \(=\lambda\)
ここで\(\lambda\)は黄金比\(\phi\)の逆数でしたね。
では、早速結果を示します:
■リトレース:Fib 23.6%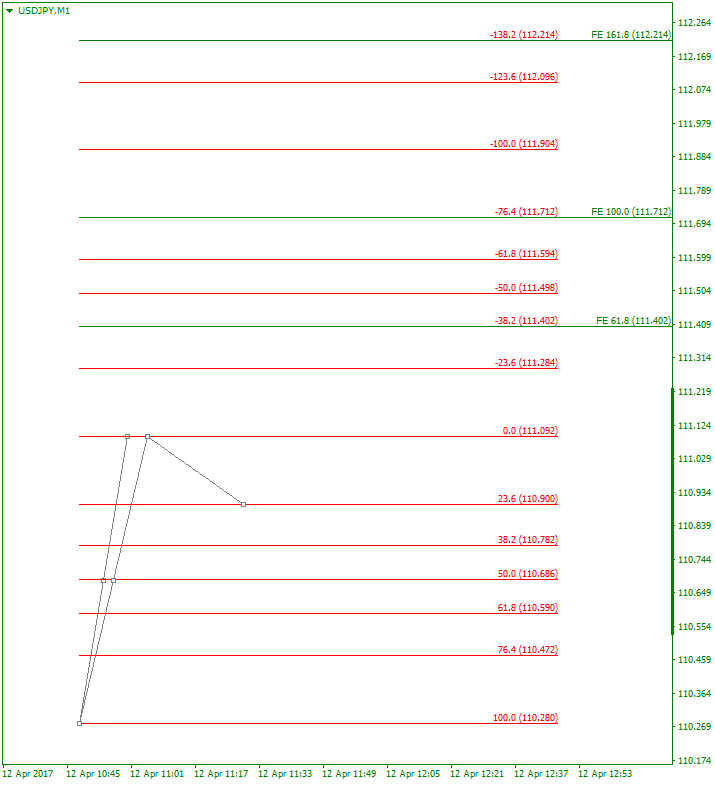
■リトレース:Fib 38.2%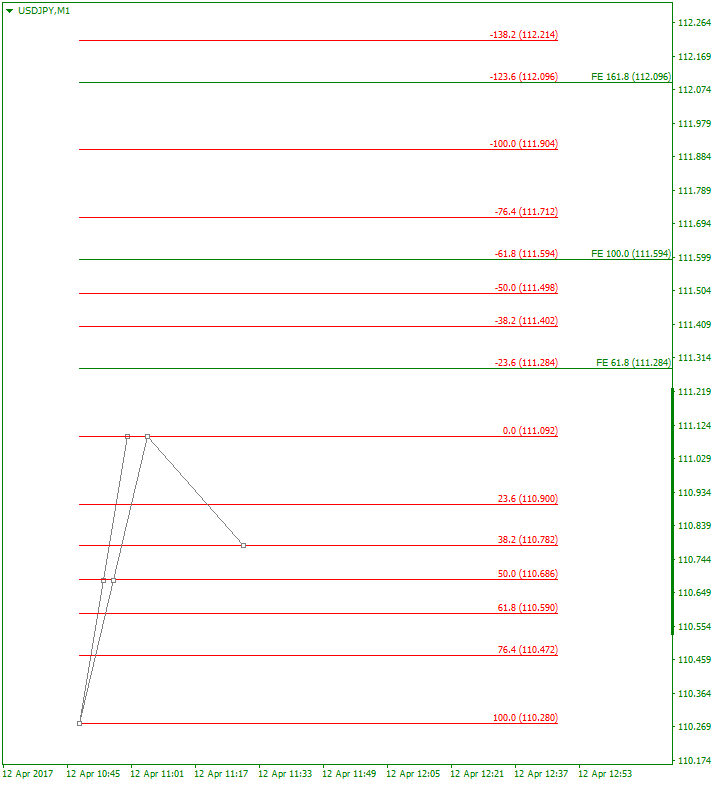
■リトレース:Fib 61.8%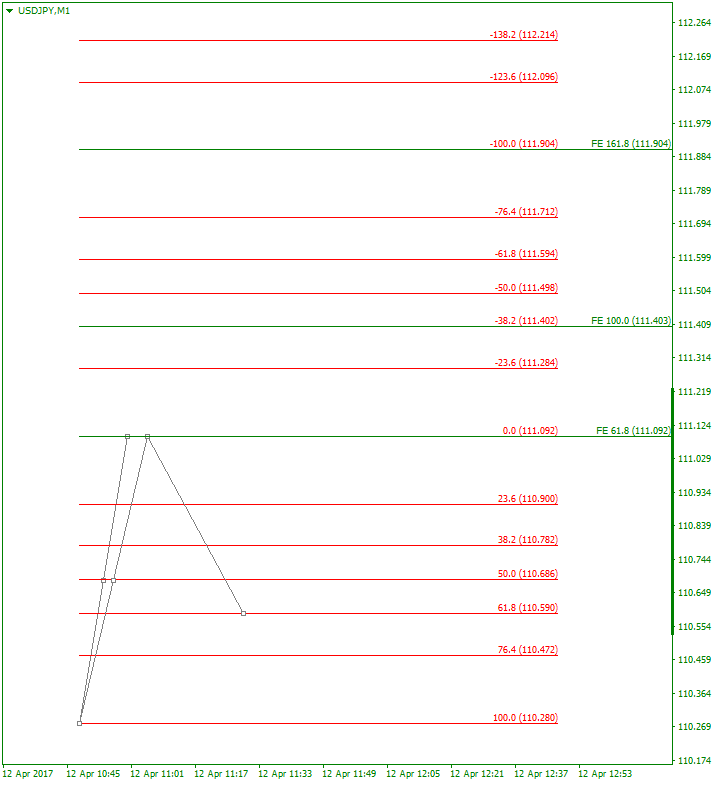
全てのケースにおいて、FEの各ラインがマイナスのフィボのいずれかのラインと合致していることがわかります。
結果を表にまとめるとこのようになります:
| リトレースの深さ | FEとマイナスのフィボとの対応関係 | ||
| FE 061.8% | FE 100.0% | FE 161.8% | |
| 23.6%\(=\lambda^3\) | -38.2%\(=-\lambda^2\) | -76.4%\(=\lambda^3-1\) | -138.2%\(=-(1+\lambda^2)\) |
| 38.2%\(=\lambda^2\) | -23.6%\(=-\lambda^3\) | -61.8%\(=-\lambda\) | -123.6%\(=-(1+\lambda^3)\) |
| 61.8%\(=\lambda\) | 0.0%\(=0\) | -38.2%\(=-\lambda^2\) | -100.0%\(=-1\) |
この対応関係が感覚的にわかっていると、フィボ(マイナスを含む)を引いただけで、わざわざ追加でFEを引かなくても、リトレースの深さに応じたFEのレベルが見えてくるようになります。
もちろん、一般にリトレースの深さはFibの各レベルぴったりになるわけではないので、正確なFEのレベルを知るためには、きちんとFEを引く必要はありますが。
それとは別に、FEとマイナスのフィボでは使い勝手に差が出てくる部分があります。
その点については、次回お話ししますので、どうぞお楽しみに♪
では、ポチっと応援お願いします☆
