こんにちは、マイクです。

昨日の記事では、

下のチャートのように、ボリンジャーバンドが完全に水平な「究極のレンジ状態」を示すのは、値動きがどんな条件を満たす時か？

という問題を出しましたね。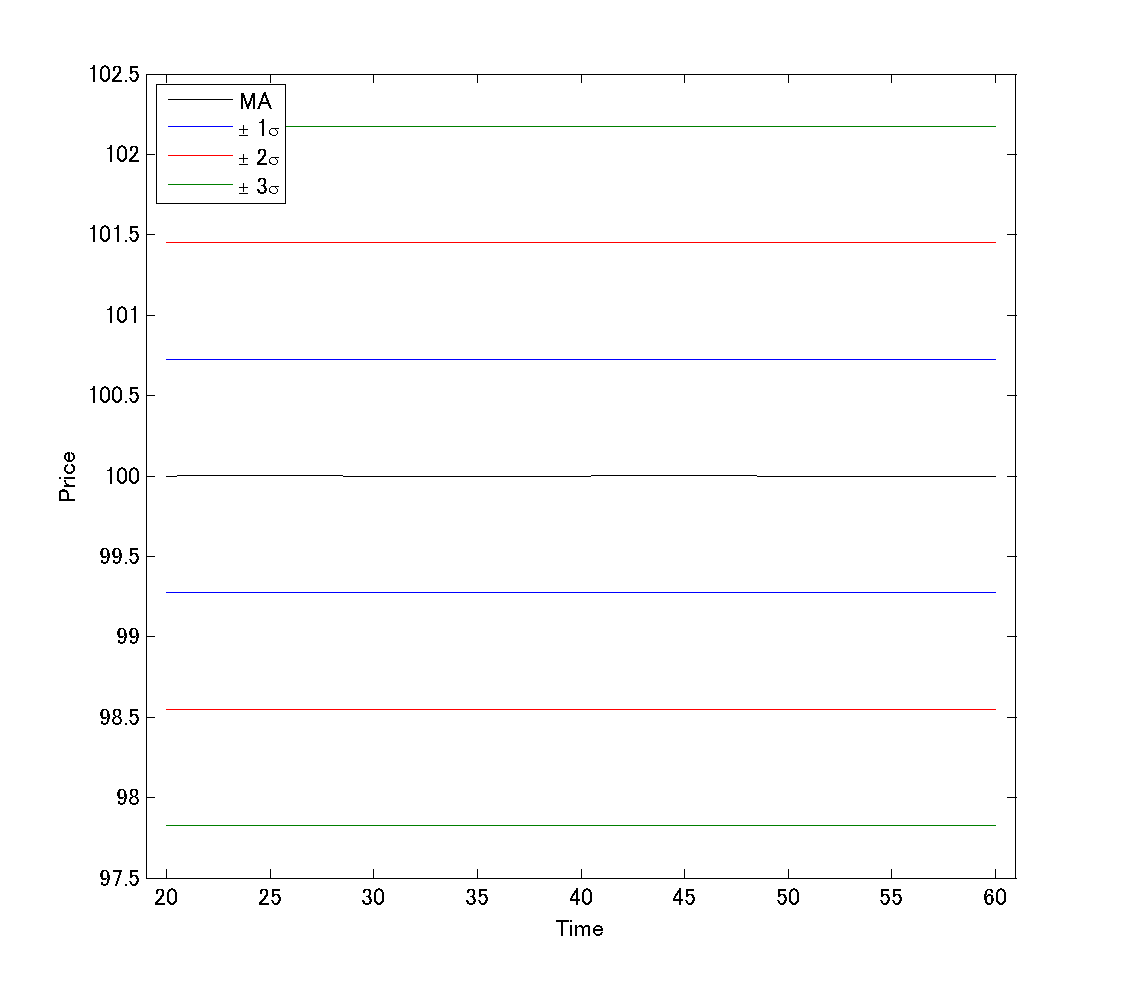


みなさん、答は考えましたか？


正解は：


その周期の整数倍がボリンジャーバンドの期間となるようなサイン波に定数を加えた形に値動きがなっている場合

です。

式で書くと、ボリンジャーバンドの期間が\(T\)の時、時刻\(t\)でのプライス\(p(t)\)が、下記のように表される場合です。

\[p(t)=a \sin\left(\frac{2n\pi}{T}t-\phi\right)+c\tag{1}\]

但し、\(n\)は自然数、\(\phi\)は任意の位相、\(c\)は任意の定数です。


\(n=1\)の場合、つまり、サイン波の周期とボリンジャーバンドの期間が一致する場合には、次のチャートのようになります。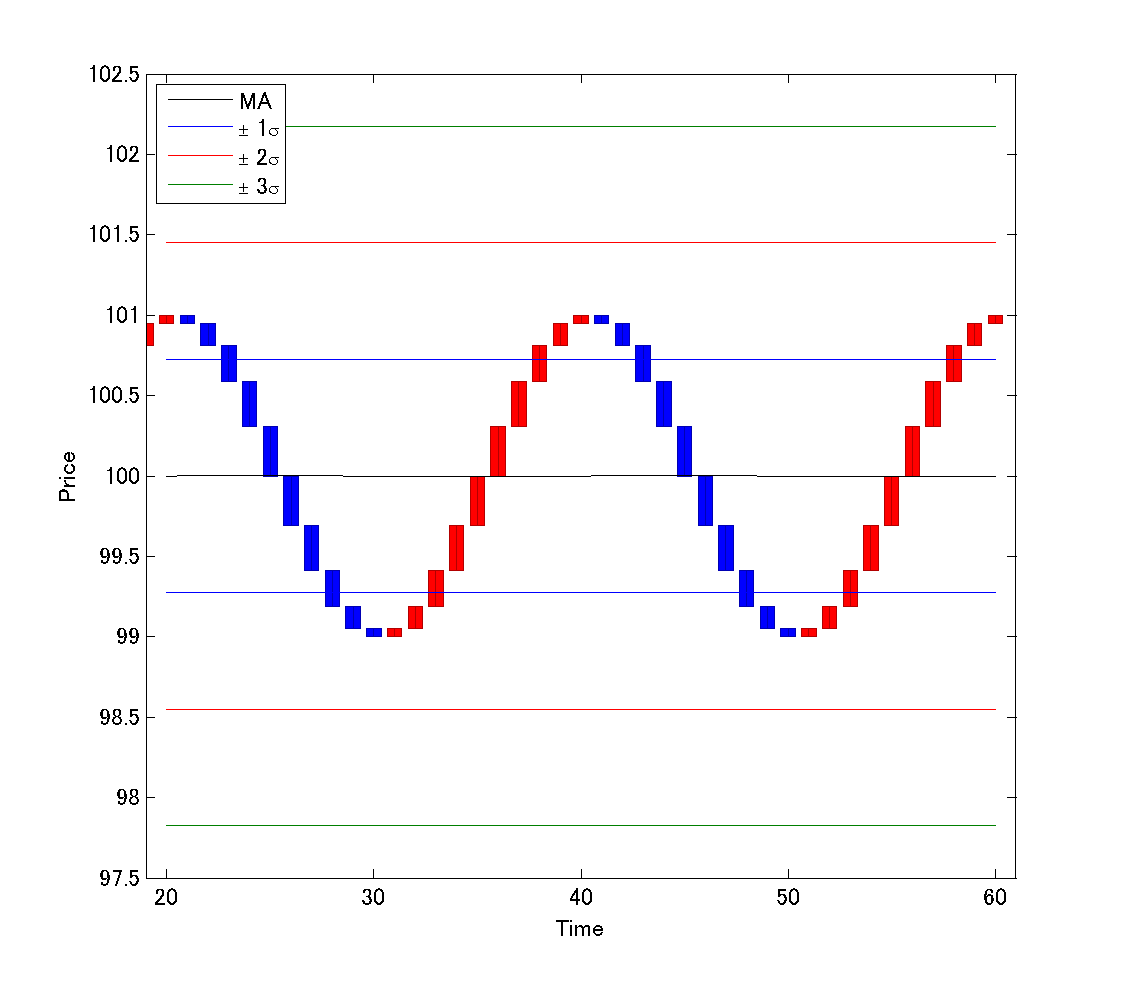


この場合、\(T=20\)、\(a=1\)、\(c=100\)です。

では、どうして値動きがこういう動きをする時には、ボリンジャーバンドが完全に水平になるのでしょうか？


それを確かめるため、実際に期間\([t-T, t]\)における平均\(\mu\)と標準偏差\(\sigma\)を求めてみましょう。

\[\mu(t)=\int_{t-T}^t p(\tau)d\tau=c\tag{2}\]

\[\sigma(t)=\sqrt{\int_{t-T}^t(p(\tau)-\mu(t))^2d\tau}=\frac{a}{\sqrt{2}}\tag{3}\]

となり、\(t\)によらず一定の値となります。

よって、全てのバンドが水平となるわけですね。


さて、ここで式(3)を変形すると、

\[a=\sqrt{2}\sigma\tag{4}\]

となりますが、これは波の振幅が\(\sqrt{2}\sigma=1.414\sigma\)であることを示しています。


よく、

「レンジの時はプライスが\(\pm1\sim 2\sigma\)を往復運動する」

と言われますが、その根拠はここにあります。


では、\(n\)が1より大きくなると、つまり、波の周期が\(1/n\)に短くなると、一体どんな感じになるのでしょうか？

次回までに想像してみてください♪


では、今日もポチっと応援お願いします☆
↓↓↓↓↓↓