こんにちは、マイクです。

一旦は軟着陸するかと思われていたギリシャ問題ですが、また緊迫した情勢になってきましたね。

週末に開かれた緊急のユーロ圏首脳会議で、ギリシャのチプラス首相は、債権者の主要な要求を3日間のうちに法制化するよう要求されましたが、これはギリシャにとってはなかなか受け入れ難い内容です。

ギリシャのEU離脱が再び現実味を帯びてきました。

今週もニュース・要人発言には注意しながらのトレードとなりますね。


さて、そんなファンダメンタルズからは少し離れて、今週はまたボリンジャーバンドを数理的側面から取り上げたいと思います。

前回のシリーズ「ボリンジャーの都市伝説」(1)、(2)、(3)、(4)、(5)では、
ボリンジャーの各バンド内に値動きが収まる確率についての定説が、全く根拠のない間違いであることを示しましたが、今回は、より基本的なボリンジャーバンドの数理的性質を探ってみたいと思います。


よく、「レンジ相場」の見分け方として、「ボリンジャーバンドが水平でバンド幅が一定」という状態が挙げられます。


その究極の状態が下のチャートとなります。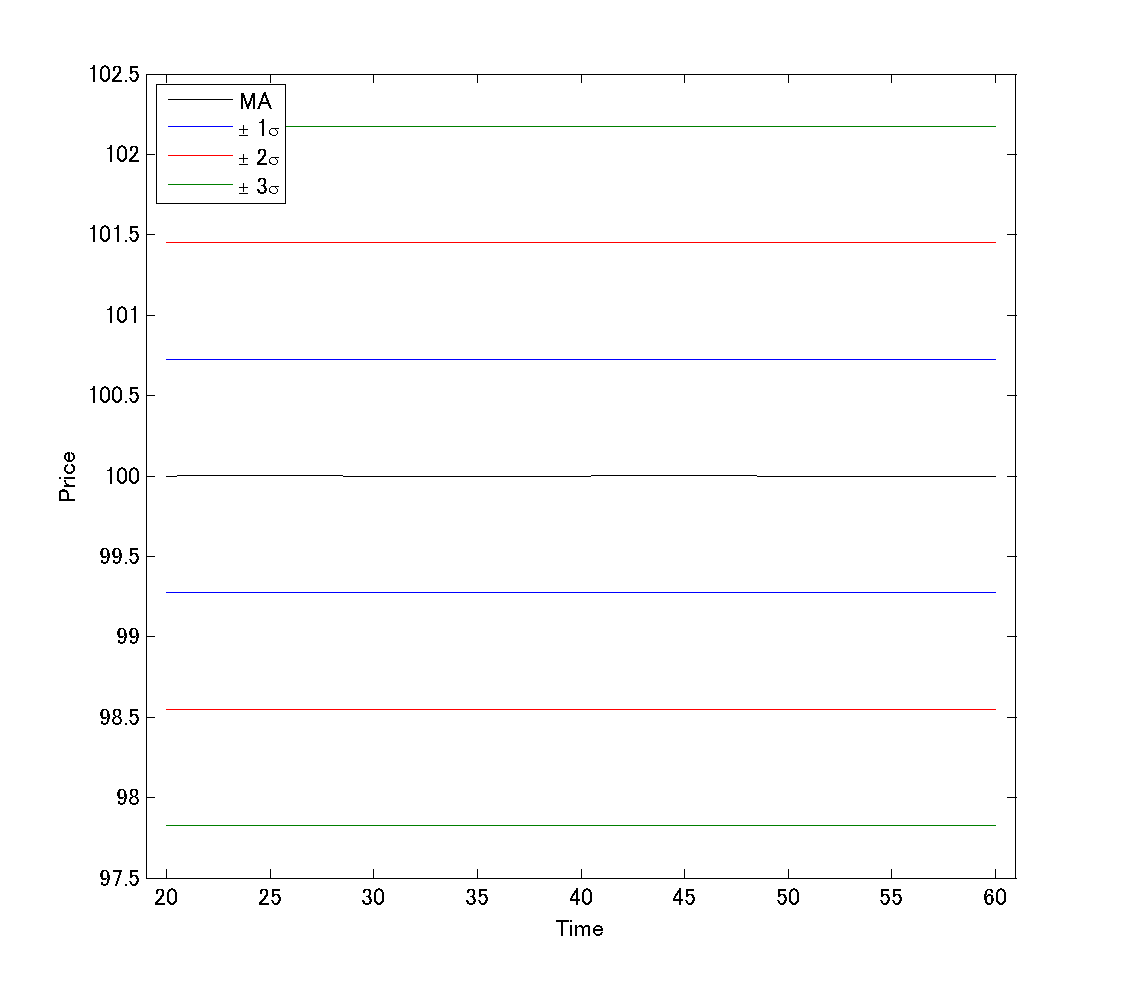

MAも各バンドも全て完全に水平になっていますね！

これは究極のレンジ状態と言えます。


さて、お気づきかと思いますが、このチャートには値動き（ローソク足）を表示していません。

実は、ボリンジャーバンドがこのように完全に水平な状態となるのは、値動きが特定の条件を満たした時に限られます。

それは一体、どんな場合でしょうか？


次回までに考えてみてくださいね！

答は1通りではありませんよ♪


では、今日もポチっと応援お願いします☆
↓↓↓↓↓↓