こんにちは、マイクです。

昨日の記事では、

ボリンジャーバンドが完全に水平な「究極のレンジ状態」を示すのは、

その周期の整数倍がボリンジャーバンドの期間となるようなサイン波に定数を加えた形に値動きがなっている場合

であることを説明し、波の周期とボリンジャーバンドの期間が等しい場合の下記チャートを示しました：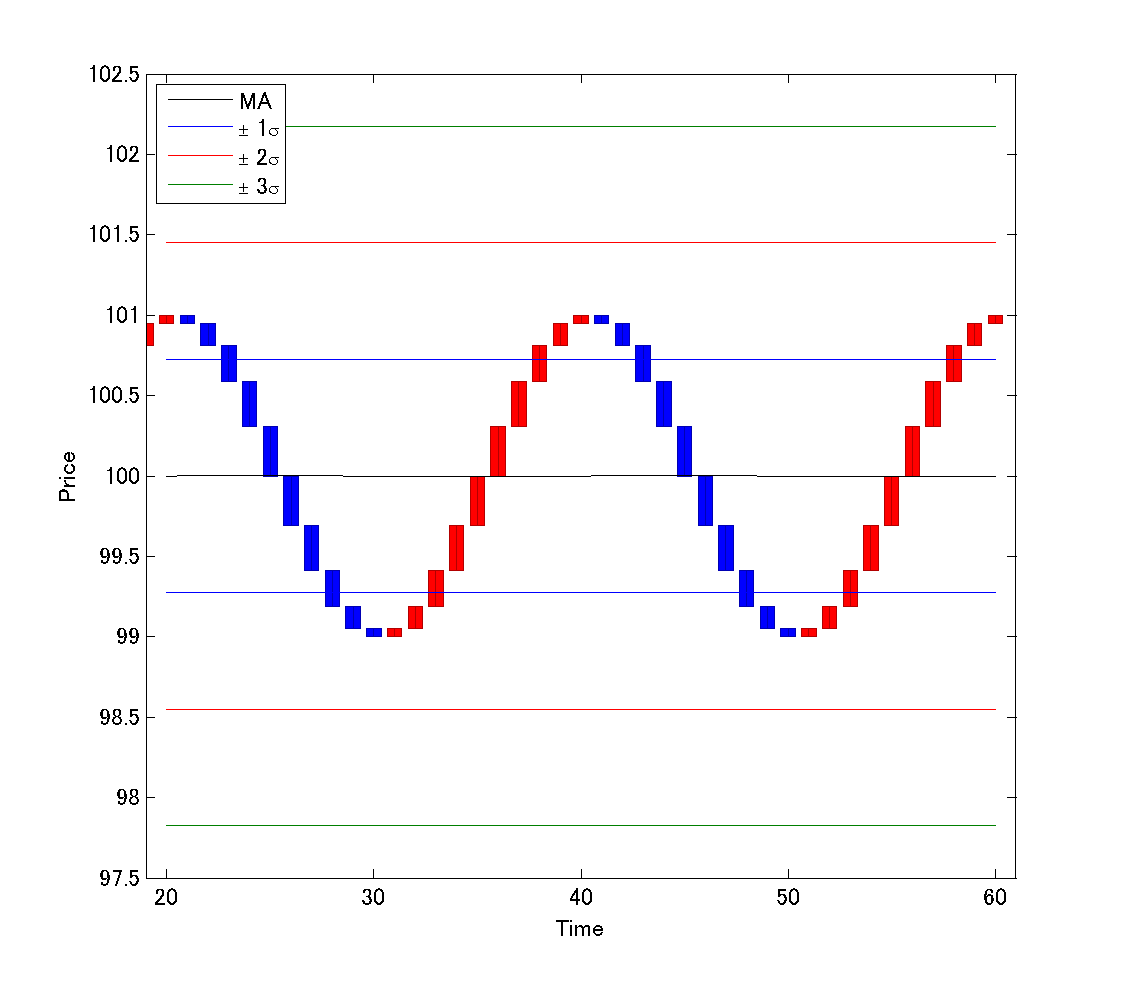


今回は、波の周期が\(1/n\)に短くなった場合にどうなるか、見てみましょう。


まず、周期が\(1/2\)になると、下記のようになります：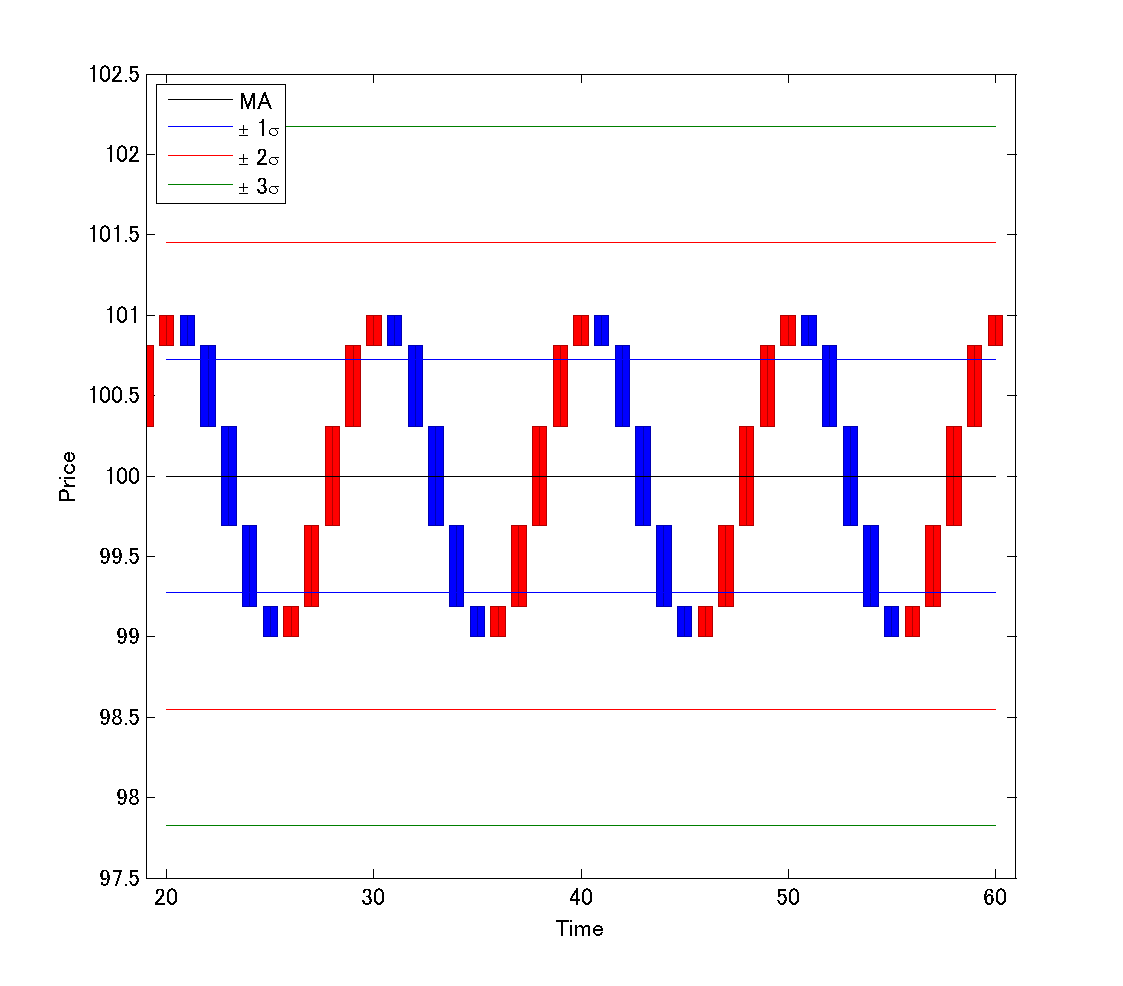

振幅とバンドの位置関係も\(n=1\)の時とほぼ同じですね。


では、極端に周期を短くして、\(1/10\)にしたら、どんな風になるでしょうか？


ちょっと想像してみてください。


しましたか？


いきますよ。


こうなります：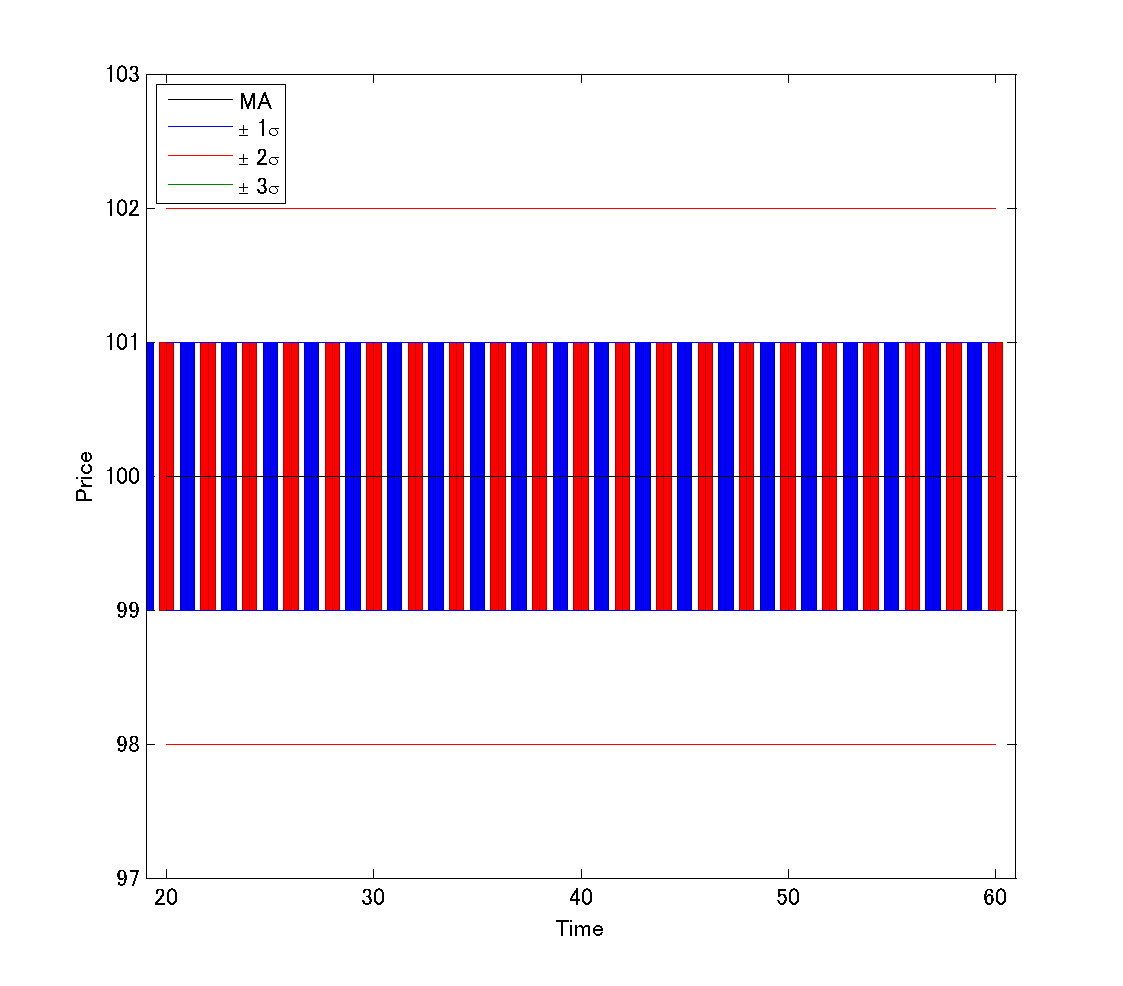


これはまるでシマウマですね！

ボリンジャーバンドの期間20の\(1/10\)ということは、周期が2だということです。

つまり、陽線と陰線の組で一つの周期が構成されているということですね。

すると、期間内の終値は、101と99が交互に10回ずつとなります。


この場合、標準偏差を計算すると、ちょうど1になります。

それで、陽線と陰線がピッタリ\(\pm1\sigma\)で挟まれた格好になっているわけですね。

シマウマの\(1\sigma\)サンドです。笑


さて、レンジ状態の話はこのくらいにして、次回からはトレンド状態の話に移りましょう♪


では、今日もポチっと応援お願いします☆
↓↓↓↓↓↓