こんにちは、マイクです。

先日の記事で示したドル円のフラクタル解析の結果については反響が非常に大きく、

「是非、他の通貨ペアについても解析結果を見せてください」

という要望を多数頂きました。

はい♪

では、ご要望にお応えして、ユーロドルの結果も公開します。


2014年のユーロドル1分足終値データ、366721個を用いたフラクタル解析です。

時系列を表示すると下のようになります。



このデータセットに対し、粗視化スケール (k=1, 5, 15, 30, 60, 240) (それぞれ、1分足、5分足、15分足、30分足、1時間足、4時間足に対応)毎に、距離 (L(k)) を求め、グラフにプロットしたのが下の図です。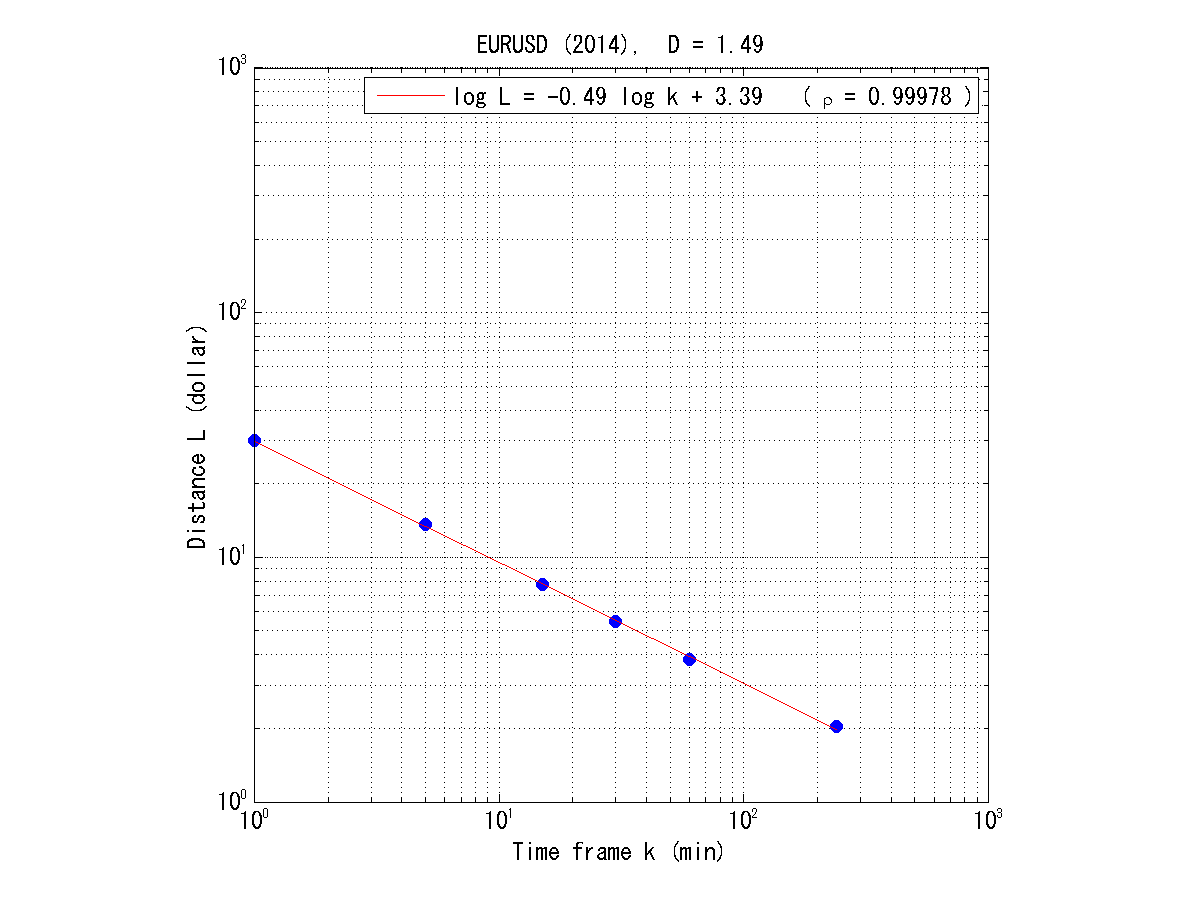



ドル円の結果と同様、プロットが完全に直線上に乗っていますね。

相関係数も0.99978と、非常に高い値となっています。

通常、フラクタル性の判定には、相関係数0.999以上が目安とされますので、このデータも、完全なフラクタルだと判定できます。


そして、直線の傾きから求めたフラクタル次元の値についても \(D=1.49\) となっており、ドル円の場合と同様、1次元ランダムウォークのフラクタル次元1.5と極めて近い値になっています。


この結果で、世界で最も流通量の多い通貨ペアであるユーロドルについても、そのフラクタル性とランダムウォーク性が示されました。


先日の記事でも触れたように、「マイクの神器」は、相場のランダムウォーク性を前提とし、その中でフラクタル性を応用したマルチタイムフレームの枠組みで、確率論的に優位性を積み上げるように設計されています。

前回までの結果と併せて、「マイクの神器」の極めて高い有効性が、更に強く支持される結果となりました♪


では、今日もポチっと応援お願いします☆

↓↓↓↓↓↓