こんにちは、マイクです。

前回の記事では、特徴的な3つのオシレータである

• RSI (Relative Strength Index)
• RCI (Rank Correlation Index)
• CCI (Commodity Channel Index)

を実際のチャートで比較しました：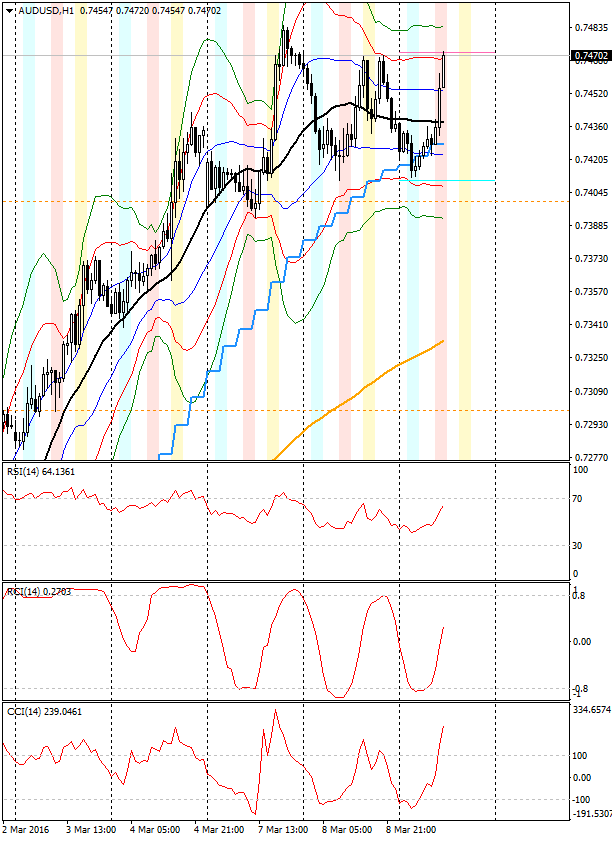



今回から、それぞれの特徴を詳しく掘り下げていきます。

まず今日は

• RSI (Relative Strength Index)

を取り上げます。


期間\(N\)のRSIの定義は以下の通りです：

\[\mathrm{RSI}(t)=100\,\frac{U(t)}{U(t)+D(t)}\tag{1}\]

ここで、

\[U(t)=\frac{N-1}{N}U(t-1)+\frac{1}{N}\max\{p(t)-p(t-1),0\}\tag{2}\]

\[D(t)=\frac{N-1}{N}D(t-1)+\frac{1}{N}\max\{p(t-1)-p(t),0\}\tag{3}\]

但し、\(p(t)\)は時刻\(t\)の終値です。


式(2)における\(\max\{p(t)-p(t-1),0\}\)は、現在の終値が一つ前の終値より大きければその増分を、小さければ0を取ります。

そして式(2)の形は指数移動平均を表し、その平滑化係数が\(1/N\)であることがわかります。

つまり、\(U(t)\)は期間中の陽線の実体幅(陰線の場合は0)の指数移動平均なのです。


同様に、\(D(t)\)は期間中の陰線の実体幅(陽線の場合は0)の指数移動平均です。


すると、式(1)のRSIは、それらの幅の合計の中で、陽線の平均幅が占める割合をパーセンテージで示すものであることがわかります。

つまり、必然的にRSIは

\[0\le\mathrm{RSI}(t)\le100\tag{4}\]

の範囲を取ります。


ここで、\(U\)と\(D\)は単純に期間内の上昇幅・下降幅ではないことに注意が必要です。

以前の記事でも書きましたが、指数移動平均は無限に過去のデータの影響も受けるので、例え\(N\)期間中の全てのローソク足が陽線(陰線)でもRSIは100(0)にはなりません。

理論上RSIが100(0)になるのは、無限に過去から全てのローソク足が陽線(陰線)の場合だけなので、式(4)の等号が成立することは実際にはありません。


以上のことから、RSIは直近の値動きの中で平滑化された陽線成分が相対的に占める割合を表現したものと言うことができます。

だから relative strength なんですね♪


では、今日もポチっと応援お願いします☆

↓↓↓↓↓↓