こんにちは、マイクです。
少し間が空いてしまいましたが、前回のMAの話では、EMAを実際に計算する際に用いる式を導出し、その式がEMAの持つある重要な特徴を示していることを指摘しました。
さて、その特徴とは何でしょうか?
■知っているようで知らないMAの話(1:SMAとEMAの違い)
■知っているようで知らないMAの話(2:EMAの「期間」って何?)
■知っているようで知らないMAの話(3:SMAとEMAの重みの関係は?)
■知っているようで知らないMAの話(4:EMAの実際の計算方法)
では、期間\(n\)のEMAの計算式を再掲しましょう:
\[\mathrm{EMA}(t)=\alpha p(t)+(1-\alpha)\mathrm{EMA}(t-1)\tag{1}\]
但し、
\[\alpha=\frac{2}{n+1}\tag{2}\]
でした。
ここで、式(1)を変形すると以下のようになります:
\[\mathrm{EMA}(t)-\mathrm{EMA}(t-1)=\alpha (p(t)-\mathrm{EMA}(t-1))\tag{3}\]
式(3)の左辺は、ひとつ前の時刻からのEMAの増分、つまり、
EMAの角度
を表しています。
そして、式(3)の右辺は、現在のローソク足の終値とひとつ前のEMAとの差分に係数\(\alpha\)を掛けたものになっています。
ここで、
\[0<\alpha<1\]
なので、
- EMAの角度が正の時には、現在のローソク足の終値はEMAより上に
- EMAの角度が負の時には、現在のローソク足の終値はEMAより下に
それぞれ存在することがわかります。
そして、
- EMAの角度が0(水平)の時には、現在のローソク足の終値はEMAと一致
していることになります。
さて、ここで「マイクの定理」を思い出してください。
「マイクの定理」とは、遅行スパンとSMAの角度との関係を表す等式です。
時刻\(t\)に対応する期間\(n\)の遅行スパンとローソク足との乖離は\[D_n(t)=p(t)-p(t-n)\tag{1}\]と表される。但し、\(p(t)\)は時刻\(t\)の終値。
一方、時刻\(t\)における期間\(n\)の単純移動平均線\(\mu_n(t)\)の角度\(A_n(t)\)を考える。
隣り合ったローソク足の横軸方向の間隔を、期間\(n\)で基準化し\(1/n\)とすれば、\[A_n(t)=n(\mu_n(t)-\mu_n(t-1))\tag{2}\]と表される。
この時、\[D_n(t)=A_n(t)\tag{3}\]が成り立つ。
つまり、「マイクの定理」によれば、
- SMAの角度は、同期間の遅行スパンとローソク足との乖離に等しい
のでしたね。
これがSMAとEMAとの決定的な違いになります。
では、チャートで確認してみましょう: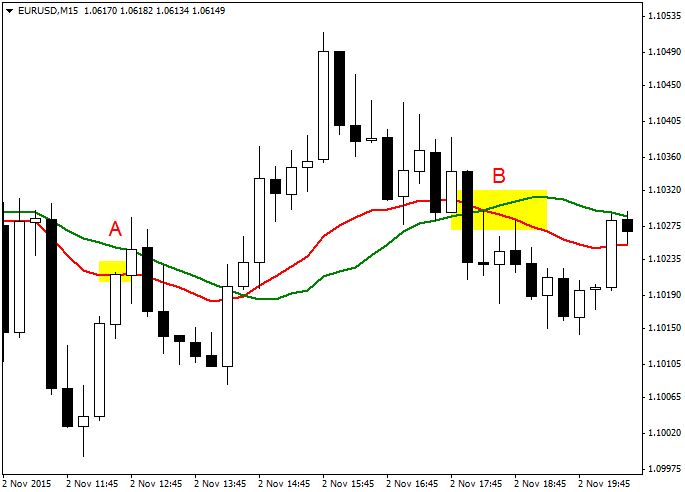
赤がEMA、緑がSMAです。
確かに、EMAの角度が負(下向き)の時はローソク足(終値)がEMAより下に、EMAの角度が正(上向き)の時はローソク足(終値)がEMAより上に、それぞれあることがわかりますね!
そして、Aのローソク足を見てください。
終値がEMAと一致していますね。
その時、EMAは確かに水平になっています!
次にBの部分を見てみましょう。
ローソク足がSMAより下にあっても、SMAは上向きのままですね。
これは遅行スパンが対応するローソク足より上にあるからです。
一方、EMAはローソク足がEMAを下回ると同時に、スパッと下向きに転じています。
これがSMAとEMAとの最も特徴的な違いです。
次回には値動きのパターン別に、2種類のMAの違いを更に見ていきたいと思いますので、お楽しみに♪
では、今日もポチっと応援お願いします☆
