こんにちは、マイクです。
オシレータ連載の前回記事では、一風変わったRCIの定義を紹介しました。
今回はその意味するものを掘り下げてみましょう。
具体例があった方がわかりやすいので、下のチャートをご覧ください:
【USDJPY】
■15分足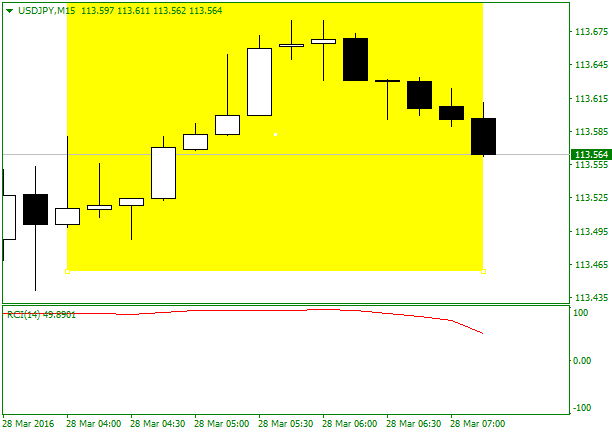
表示されているRCIの期間は14なので、黄色の範囲のローソク足が計算に使われていることになります。
この時、「時刻の順位」と「終値の順位」は以下のようになります: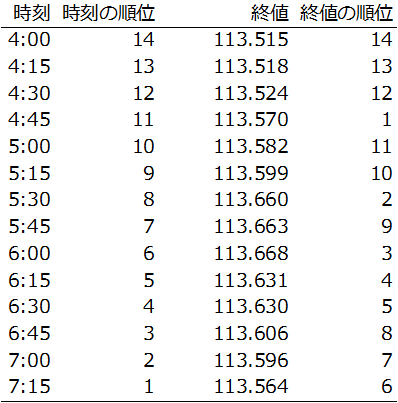
時刻の順位は、現在の足が1、一つ前が2、・・・、最も過去の足が14となります。
また、終値の順位は、最高値をつけた4:45の足が1、次に高い5:30の足が2、・・・、最も安い4:00の足が14となります。
そして、実はRCIは、この2つの順位(rank)の相関係数(correlation coefficient)を求めたものなのです!
統計学では、この順位の相関係数のことを、特別に
Spearmanの順位相関係数
(Spearman’s rank correlation coefficient)
と呼びます。
この概念を提唱した数学者Charles Spearmanにちなんだものです。
RCI (Rank Correlation Index)という名前もこれに由来しています。
ところで、前回示したRCIの定義:
\[\mathrm{RCI}(t)=100\,\left(1-\frac{\displaystyle 6\sum_{j=0}^{N-1}(d_j-p_j)^2}{N(N^2-1)}\right)\tag{1}\]
(\(N\)は期間、\(d_j\)は時刻\((t-j)\)の順位、\(p_j\)は時刻\((t-j)\)の足の終値の順位)は、本当に相関係数を表しているのでしょうか??
実際に確かめてみましょう。
\(\{d_j\}\)と\(\{p_j\}\)の相関係数を\(\rho\)とすると、標本相関係数の定義から、
\[\rho=\frac{\displaystyle\sum_{j=0}^{N-1}(d_j-\hat{d})(p_j-\hat{p})}{\displaystyle\sqrt{\left(\sum_{j=0}^{N-1}(d_j-\hat{d})^2\right)\left(\sum_{j=0}^{N-1}(p_j-\hat{p})^2\right)}}\tag{2}\]
ここで、\(\hat{d}\)は\(\{d_j\}\)の平均、\(\hat{p}\)は\(\{p_j\}\)の平均。
ところで、\(\{d_j\}\)も\(\{p_j\}\)も、1から\(N\)までの値を一つずつ取るので、
\[\hat{d}=\hat{p}=\frac{1}{N}\sum_{j=1}^N j=\frac{N+1}{2}\tag{3}\]
よって、
\begin{align}\sum_{j=0}^{N-1}(d_j-\hat{d})^2&=\sum_{j=0}^{N-1}(p_j-\hat{p})^2\\&=\sum_{j=1}^N\left(j-\frac{N+1}{2}\right)^2\\&=\sum_{j=1}^N\left(j^2-(N+1)j+\left(\frac{N+1}{2}\right)^2\right)\\&=\sum_{j=1}^N j^2-(N+1)\sum_{j=1}^N j+N\left(\frac{N+1}{2}\right)^2\\&=\frac{N(N+1)(2N+1)}{6}-\frac{N(N+1)^2}{2}+\frac{N(N+1)^2}{4}\\&=\frac{N(N+1)(N-1)}{12}\tag{4}\end{align}
また、
\[\sum_{j=0}^{N-1}(d_j-\hat{d})(p_j-\hat{p})=\sum_{j=0}^{N-1}d_j p_j-\frac{N(N+1)^2}{4}\tag{5}\]
一方、
\[\sum_{j=0}^{N-1}(d_j-p_j)^2=-2\sum_{j=0}^{N-1}d_j p_j+\frac{N(N+1)(2N+1)}{3}\tag{6}\]
なので、結局、
\[\sum_{j=0}^{N-1}(d_j-\hat{d})(p_j-\hat{p})=-\frac{1}{2}\sum_{j=0}^{N-1}(d_j-p_j)^2+\frac{N(N+1)(N-1)}{12}\tag{7}\]
となります。
よって、式(4)・(7)を(2)に代入すると、
\[\rho=1-\frac{\displaystyle 6\sum_{j=0}^{N-1}(d_j-p_j)^2}{N(N^2-1)}\tag{8}\]
となり、パーセンテージ表示にするために100を掛けると、RCIの定義に一致しました!![]()
あー、ちょっと疲れましたね。笑
次回は、RCIが相関係数であることによって生じる特徴について見ていきましょう♪
では、今日もポチっと応援お願いします☆
