こんにちは、マイクです。

オシレータ連載も少し間が空いてしまいましたが、前回記事では、RCIが「順位の相関係数」であることを示しました。

復習を兼ねて、順位の相関係数とは何を意味しているのかを、視覚的に確認してみましょう。

前回と同じチャート例を使います：

【USDJPY】
■15分足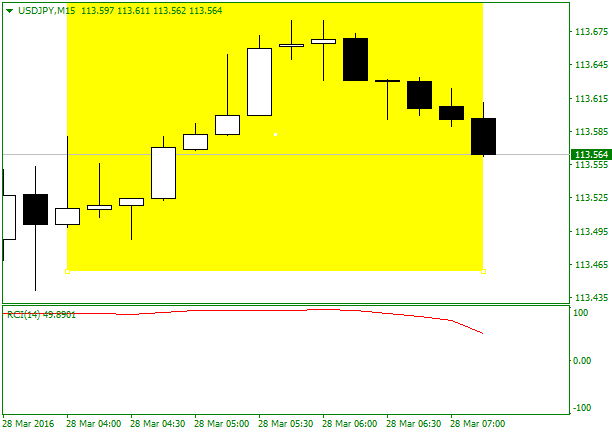

表示されているRCIの期間は14なので、黄色の範囲のローソク足が計算に使われていることになります。

この時、「時刻の順位」と「終値の順位」は以下のようになります：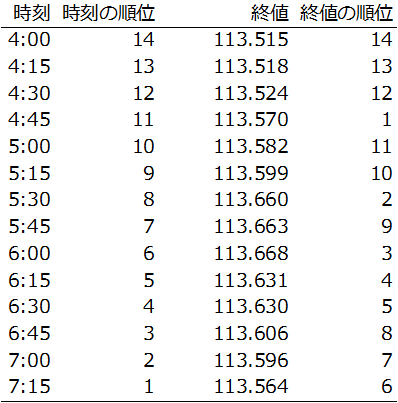



そしてRCIは、この2つの順位(rank)の相関係数(correlation coefficient)を求めたものなのでしたね。


この「相関係数」の意味をイメージするために、下の図をご覧ください：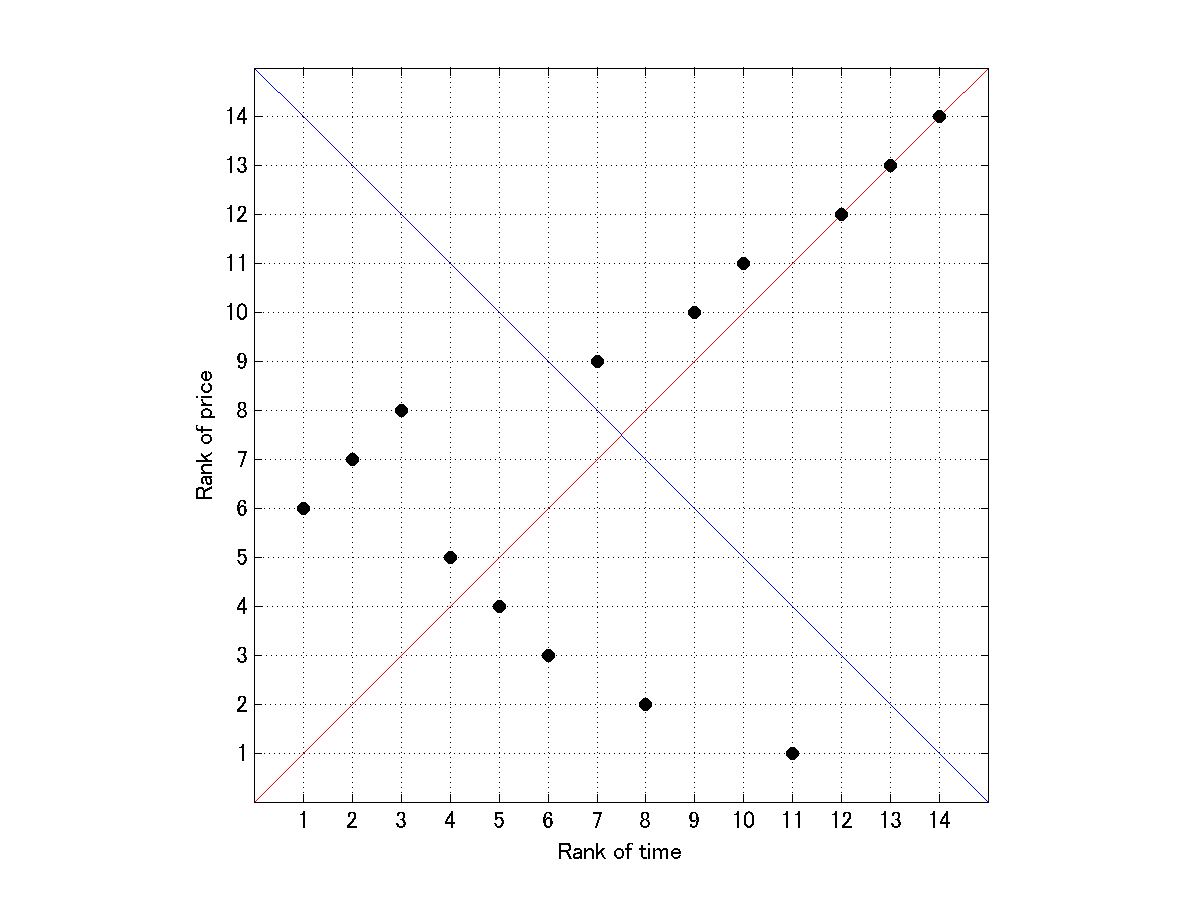


この図は、横軸に「時間の順位」を、縦軸に「価格の順位」を取って、14期間のデータをプロットしたものです。

もし、この図で、全てのプロットが赤い線上にあった場合、「時間の順位」と「価格の順位」が完全に一致することとなり、この時、相関係数の値は

RCI=100%

となります。

逆にもし、全てのプロットが青い線上にあった場合、「時間の順位」と「価格の順位」は完全に反対になり、この時、相関係数の値は

RCI=-100%

となります。

今回のデータは、どちらかというと赤い線に沿っているものが多いので、RCIの値は0より大きくなっているわけですね(RCI=50%)。


さて、では、RCIが相関係数であることによって、どのような特徴が生じるでしょうか？


・・・


考えましたか？


まず、相関係数の性質から、価格がRCIの期間にわたって上昇し続ければRCI=100%、下降し続ければRCI=-100%となります。

これはRSIが±100%には現実的には到達しないのと大きく違うところです。


次に、RCIの値は価格の順位のみに依存し、値幅には左右されません。

例えば、大きく下落した後、ごく浅い戻しでも、RCIの期間だけ戻し続ければ、RCIの値は100%となります。

これも、RSIとは対照的ですね。


これらの特徴の結果、RCIは値幅的にはごく浅い押し戻しでも、その状態で時間が経過すれば、非常に敏感に反応するという性質を持つことになります。


この性質は、検出力の高さという意味ではメリットですが、結果的にダマシに遭う危険性も孕んでいます。

この点を補うために、

異なる期間のRCIを同時に表示する

ことがよく行われます。


それによって、「木を見て森を見ず」状態になることを避けているわけですね♪


では、今日もポチっと応援お願いします☆

↓↓↓↓↓↓