こんにちは、マイクです。
これまで、
特徴的な3つのオシレータ
- RSI (Relative Strength Index)
- RCI (Rank Correlation Index)
- CCI (Commodity Channel Index)
のうち、RSIとRCIについて、その定義と特徴を解説してきました。
今日は最後のCCIについて見ていきましょう。
■オシレータの数理(1:特徴的な3つの指標を見てみよう)
■オシレータの数理(2:RSIの定義と特徴)
■オシレータの数理(3:一風変わったRCIの定義)
■オシレータの数理(4:RCIは順位の相関係数)
■オシレータの数理(5:相関係数であるRCIの特徴)
まず、もう一度、3つのオシレータのチャートをご覧ください: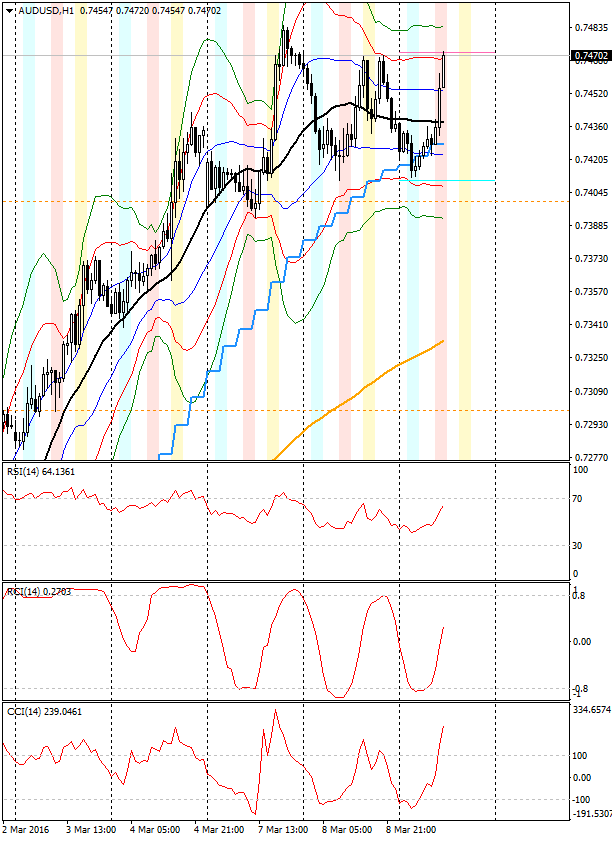
これを見ると、CCIは他の2つに比べて随分急激な動きをしていますね。
その理由を調べるため、CCIの定義を確認しましょう。
期間\(N\)のCCIは次式で表されます:
\[\mathrm{CCI}(t)=\frac{p(t)-\mu(t)}{0.015\sigma(t)}\tag{1}\]
\[p(t)=\frac{\mathrm{H}(t)+\mathrm{L}(t)+\mathrm{C}(t)}{3}\tag{2}\]
\[\mu(t)=\frac{1}{N}\sum_{j=0}^{N-1}p(t-j)\tag{3}\]
\[\sigma(t)=\frac{1}{N}\sum_{j=0}^{N-1}|p(t-j)-\mu(t)|\tag{4}\]
\(p(t)\)は基準値(typical value)と呼ばれ、時刻\(t\)のバーの高値(H)・安値(L)・終値(C)の平均です。
Pivot pointと同じですね。
そして、\(\mu\)は\(p\)のN期間移動平均、\(\sigma\)は平均偏差です。
平均偏差は標準偏差に似ていますが、2乗和の平方根ではなく、絶対値の平均を使うところが異なります。
式(1)を見ると、CCIは基準値とその移動平均との乖離を平均偏差で基準化したものであることがわかりますね。
平均偏差に掛かる係数が0.015なので、乖離が平均偏差の1.5倍の時に、CCIは±100となります。
次回は、この定義から出てくるCCIの特徴を見ていきましょう♪
では、今日もポチっと応援お願いします☆

FXにおける機械学習の有効性について。
マイクさんこんにちは。
マイクさんがfxで機械学習を試された経験が
お有りでしょうか?
私、EA等で手法・ルールをプログラミングしても
その限界を感じております。
最近、aiが流行しており、色々調べていくと
機械学習という言葉を知り更に、既にだれでも
使えるプラットフォームまで用意されています。
私は確率、統計は詳しくありません。
そこでマイク博士にその見解や可能性のご意見を
伺う所存です。
お忙しいところ恐縮ですが、お願い致します。
cool island さん、こんにちは。
EAに機械学習を実装することは、まさに現在マイクの研究課題となっています。
特に、関連ベクトルマシン(relvance vector machine, RVM)によるパターン分類は、適切な事前学習を行えば、かなり有効に機能する感触を得ています。
いずれにしても、今後のトレーディングプログラムにおいて、ベイズ理論に基づく機械学習が重要な役割を担うことは間違いないですね。
またブログ記事でも関連した話題を取り上げていきたいと思います。
ご質問、ありがとうございました♪