こんにちは、マイクです。

昨日の記事では、プライスが等速運動する「究極のトレンド状態」では、全ての時間足でローソク足がBB+1σと+2σの間（上昇トレンドの場合。下降の場合はBB-1σと-2σの間）でバンドウォークするという普遍性を持っていることを説明しました。

今日は、どうしてこのような普遍性が表れるのかを解明しましょう。

話を単純化するために、ボリンジャーバンドの期間の間に、価格\(x\)が\(-a\)から\(a\)まで動いたとします。

すると、現在の価格は\(a\)、MAの値\(\mu\)は0ですね。

\[\mu=\int_{-a}^a \frac{1}{2a} x dx = 0\]

では、バンド幅σはいくつになるでしょうか？

計算してみましょう。

\[\sigma^2=\int_{-a}^a \frac{1}{2a} x^2 dx = \left[ \frac{1}{6a} x^3\right]_{-a}^a = \frac{a^2}{3}\]

よって、

\[\sigma = \frac{a}{\sqrt{3}}\]

となります。

これを書き直すと、

\[a= \sqrt{3}\sigma \tag{1}\]

ですね。

つまり、現在の価格(終値)は必ず\(\sqrt{3}\sigma\simeq 1.73\sigma\)に位置することになります！

もう一度、時間足の異なる2つのチャートを見てみましょう：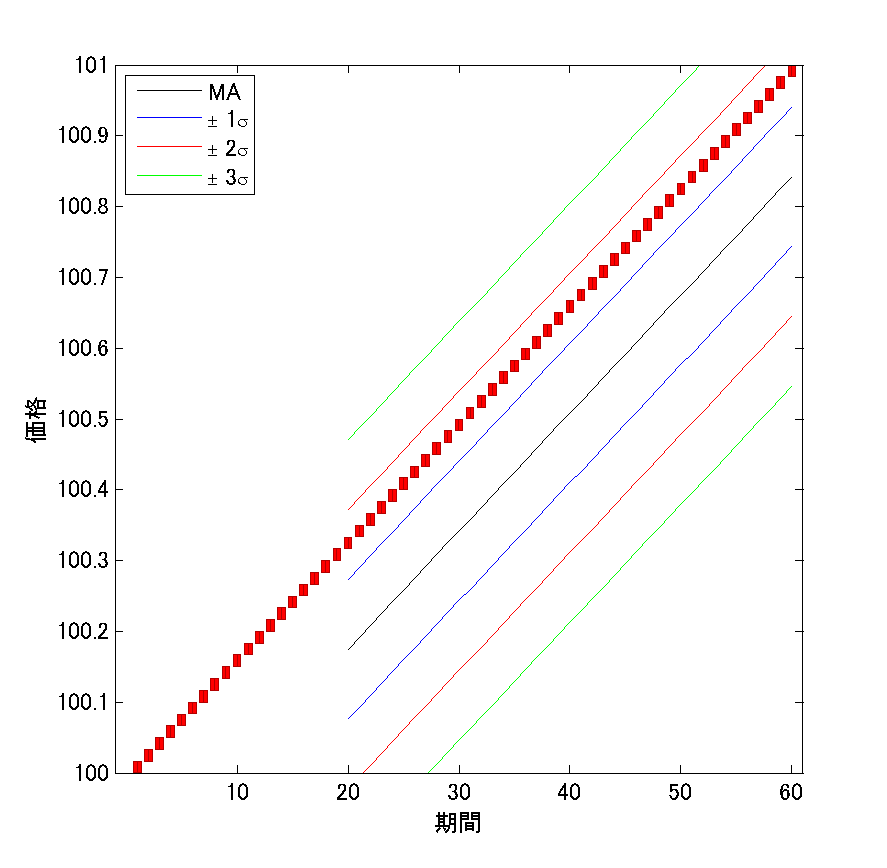



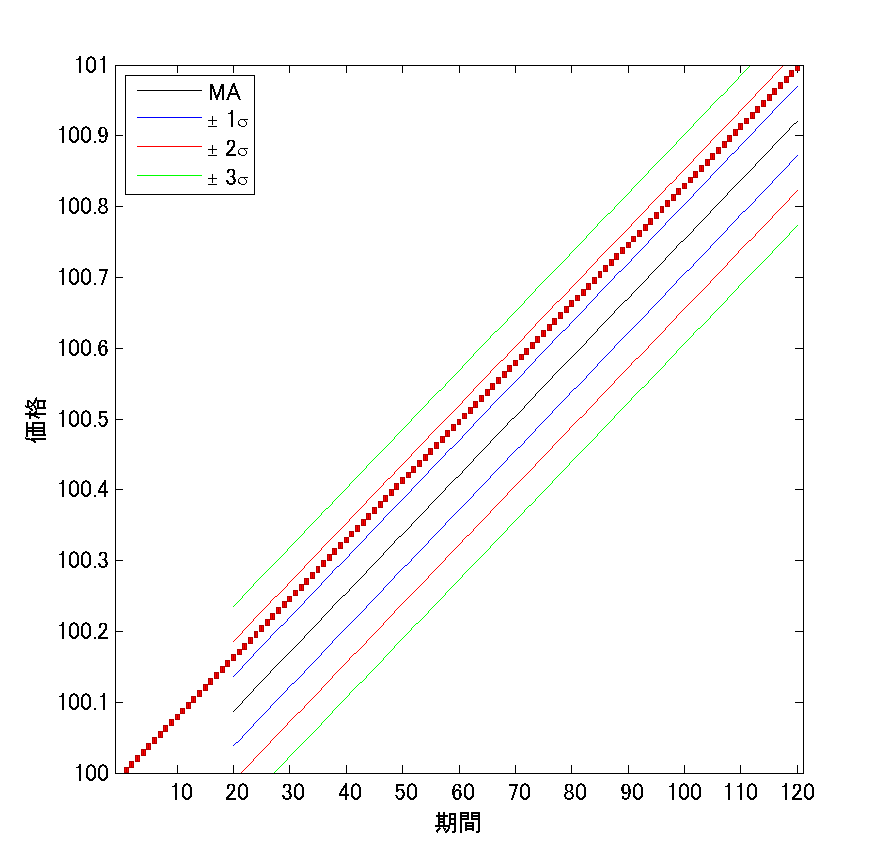
両方のチャートで、「終値」の位置に注目してください。

どちらも、\(\sqrt{3}\sigma\simeq 1.73\sigma\)に終値があることが確認できますね。

つまり、トレンド状態において、\(\pm\sqrt{3}\sigma\)は、トレンドの「加速」と「減速」の

分水嶺

となっていることがわかります。

巡航速度の時に終値がちょうど\(\pm\sqrt{3}\sigma\)に位置するのですから、\(\pm\sqrt{3}\sigma\)の外側に終値が位置する時はトレンドが加速していることを、\(\pm\sqrt{3}\sigma\)の内側に終値が位置する時はトレンドが減速していることを、それぞれ意味しているわけです。

通常、\(\pm\sqrt{3}\sigma\)にはラインを引いていないと思いますが、実はそこに分水嶺が通っていると認識してチャートを見ると、トレンドの勢いが非常にわかりやすく見えてくると思います♪


では、今日もポチっと応援お願いします☆
↓↓↓↓↓↓