こんにちは、マイクです。

前回の記事では、正弦波状の値動きに対して、SMAとEMAがそれぞれどのような形状になるかを分析しました。

今回は、価格が急変した場合について見てみましょう。

では早速、下のチャートをご覧ください。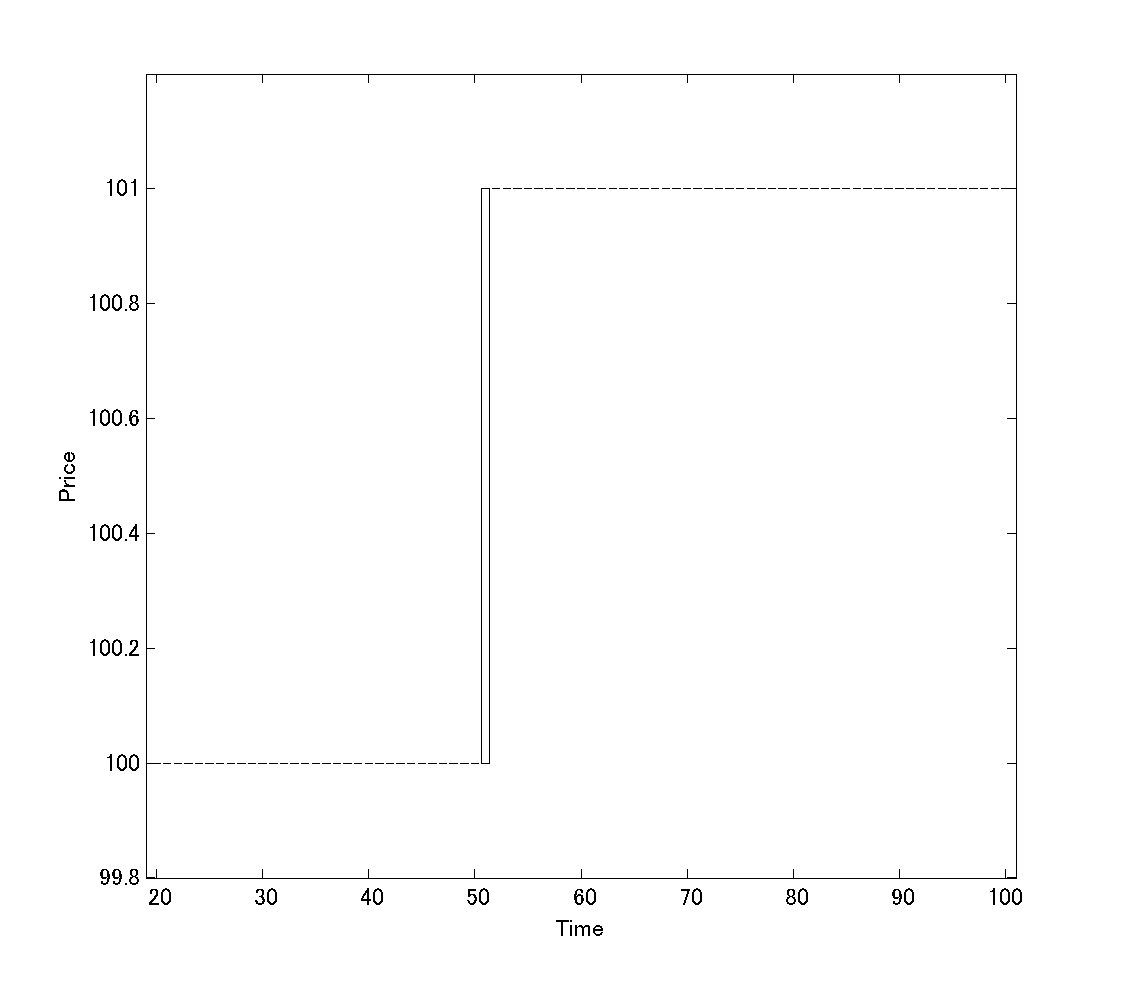

横ばいで推移してきた価格が一気に急騰し、その後また横ばいとなった状況です。

ここまで極端ではないにしても、似たような状況は実際にもありますね。


では、この値動きに対して期間20のSMAとEMAを描くと、どのような感じになるでしょうか？


今回も下の答えを見る前に考えてください。


・・・


いいですか？


では、答です：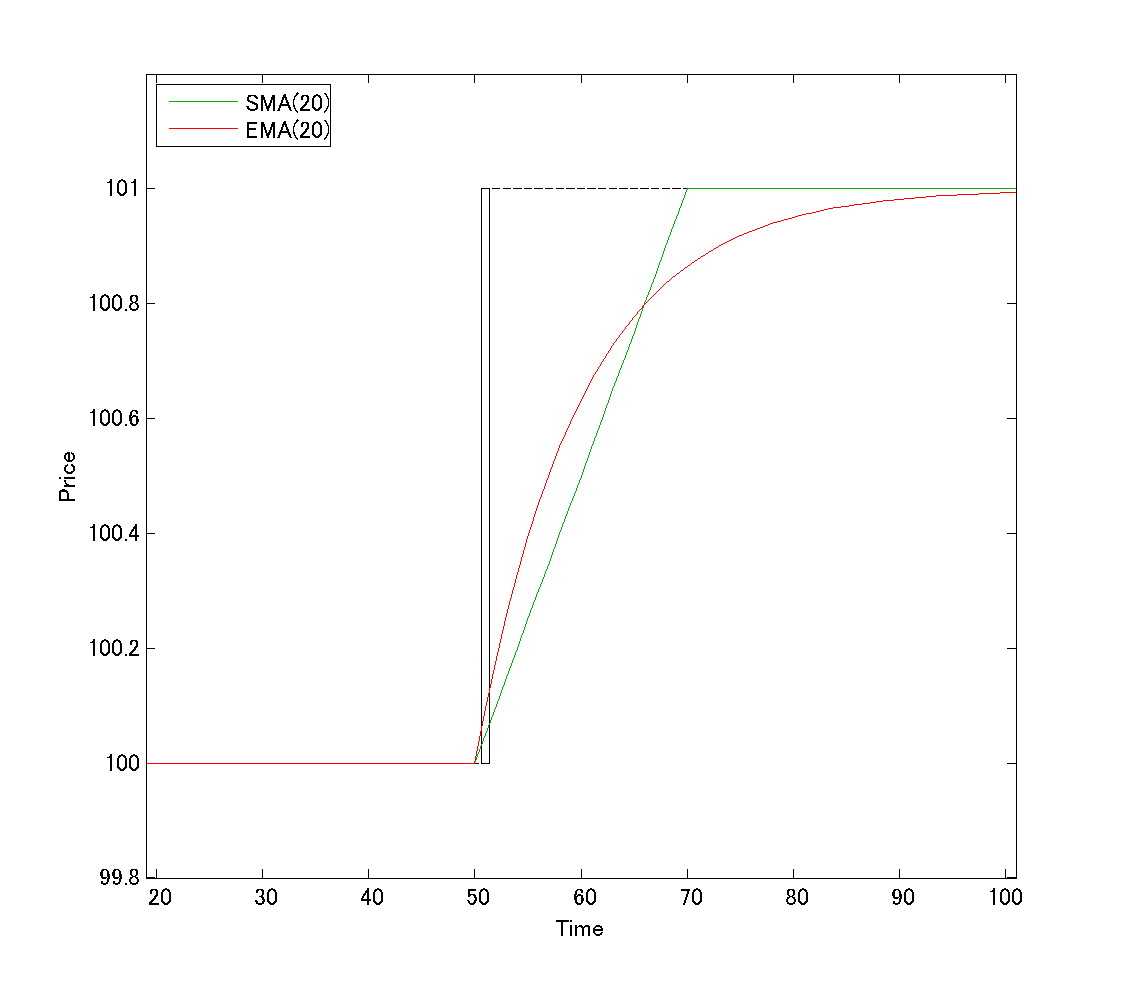

はい、今回はどうでしょう？

前回よりは想像しやすかったかも知れませんね。


この場合、SMAは、急騰前のプライスから急騰後のプライスに向け、完全に直線的に上昇していきます。

一方、EMAは、急騰直後はSMAより早く上昇しますが、だんだん上昇の角度がゆるやかになり、途中でSMAに抜かされてしまいます。

これも、前の記事で説明したように、EMAの角度が、ローソク足とEMAの乖離に比例しているからに他なりません。

そして、急騰からMAの期間の倍以上時間が経っても、まだ急騰後のプライスには到達していませんね。

EMAは平均の重みが無限に過去まで0にならないので、過去のプライスをいつまでも引きずることになります。

その点、SMAは過去をすっきり忘れてしまう性格ですね。笑

このようなMAの性格の違いを把握しておくことも、状況判断の助けとなると思います。


さて、次回は少し違った側面からMAの持つ意味を考えてみます♪


では、今日もポチっと応援お願いします☆

↓↓↓↓↓↓