こんにちは、マイクです。

今日はこれまでとは別の視点から移動平均について考察します。

移動平均とは、現在および過去の終値に重みを掛けて足し合わせたものでしたね。

期間\(n\)のSMAの場合、ローソク足の終値を入力\(u(t)\)、移動平均の値を出力\(y(t)\)と考えると、両者の間には下記の関係が成り立ちます：

\[y(t)=B(z)u(t)\tag{1}\]

ここで、

\[B(z)=\sum_{j=0}^{n-1}b_j z^{-j}\tag{2}\]

\[b_j=\frac{1}{n}\tag{3}\]

なお、\(z^{-1}\)は時間遅れ演算子で、時間を1つ過去に戻す作用があります。

つまり、

\[z^{-1}u(t)=u(t-1)\tag{4}\]

ということですね。

よって、式(2)～(4)を(1)に代入すると、

\[y(t)=\frac{1}{n}\sum_{j=0}^{n-1}u(t-j)\tag{5}\]

となり、確かにSMAの定義式と一致していることがわかります。


さて、式(1)を見て気が付いた方もいらっしゃると思いますが、このような形で表される関係を、信号処理の分野ではデジタルフィルタと呼びます。

より一般的には、\(z^{-1}\)の多項式\(A\), \(B\)に対して、入出力が

\[A(z)y(t)=B(z)u(t)\tag{6}\]

という関係で表されるものをデジタルフィルタと言い、特に、式(1)のように

\[A(z)=1\tag{7}\]

の場合をFIRフィルタ(Finite Impulse Response filter)と呼びます。

何がfinite(有限)かと言うと、入力した信号に影響を及ぼされる出力が有限個であるということを意味しています。

前回の記事で、「SMAは過去をすっきり忘れてしまう性格」と書きましたが、まさにこのことを指しているんですね。

一方、\(A\)の次数が1以上の場合にはIIRフィルタ(Infinite Impulse Response filter)と呼ばれます。


さて、式(6)で表されるデジタルフィルタにおいて、

\[H(z)=\frac{B(z)}{A(z)}\tag{8}\]

を伝達関数と言い、

\[z=e^{i\omega}\tag{9}\]

を代入することにより(\(\omega\)は角振動数)、このデジタルフィルタの周波数特性\(H(\omega)\)を求めることができます。


では、実際にSMAの周波数特性を求めてみましょう！

FIRフィルタの場合、

\[H(z)=B(z)\tag{10}\]

なので、式(2)に(9)を代入して、

\[H(\omega)=\frac{1}{n}\sum_{j=0}^{n-1}e^{-i\omega j}\tag{11}\]

という周波数特性が得られました♪


これを、SMAの期間が\(n\)=20の場合に図示すると下記のようになります：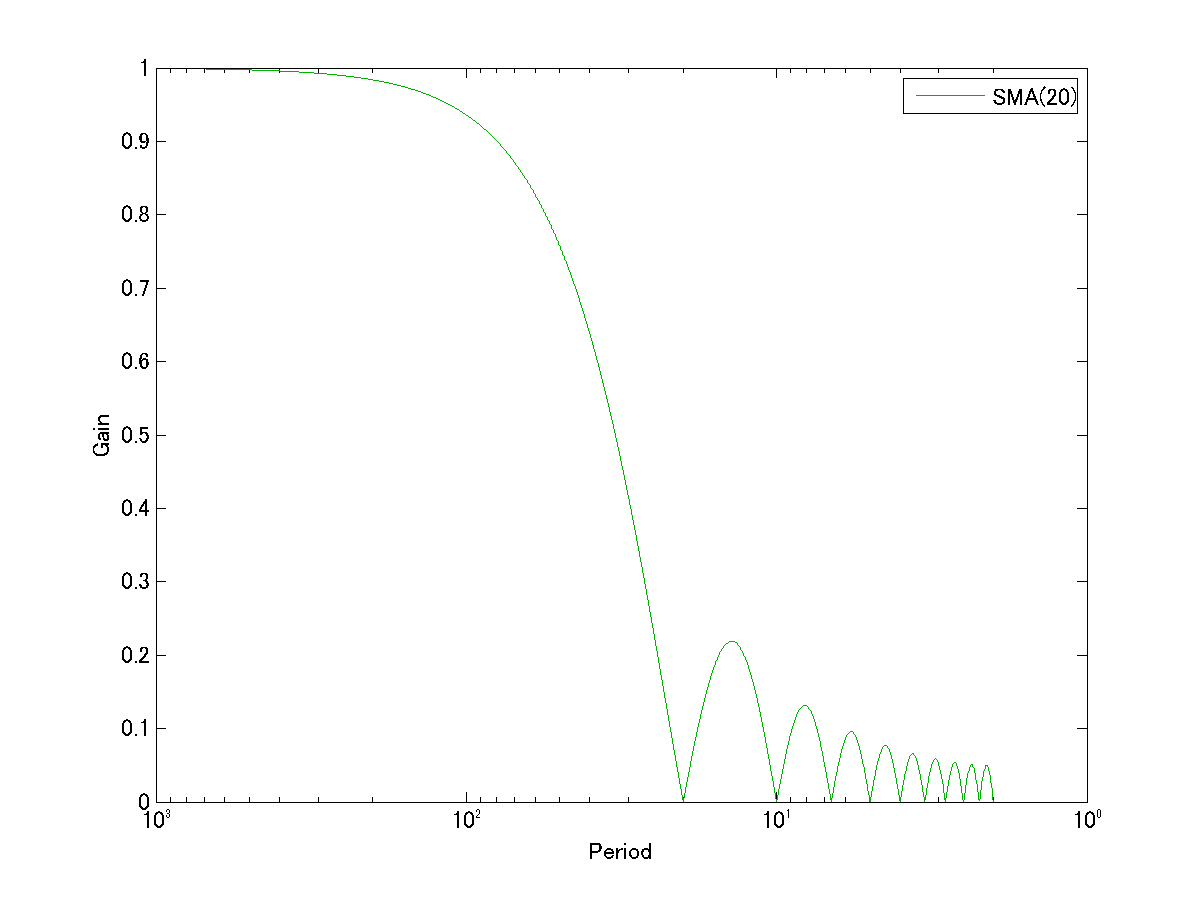


横軸はわかりやすいように角振動数ではなく周期で表しています。

また、\(H(\omega)\)は複素数なので、その絶対値を縦軸で表しています。


このグラフは、SMAの持つ特徴を非常に端的かつ明快に示しています。

詳しくは次回解説するので、どうぞお楽しみに♪


では、今日もポチっと応援お願いします☆

↓↓↓↓↓↓