こんにちは、マイクです。

久々に「オシレータ連載」の続きを書きたいと思います。

前回の記事からかなり間が空いてしまいましたね。


これまで、特徴的な3つのオシレータ

• RSI (Relative Strength Index)
• RCI (Rank Correlation Index)
• CCI (Commodity Channel Index)

の定義と特徴を順番に見てきたわけですが、今回は最後のCCIの特徴についてお話しします。

前回の記事では、CCIは基準値とその移動平均との乖離を平均偏差で基準化したものであることをその定義から示し、乖離が平均偏差の1.5倍の時に、CCIの値が±100となることを説明しました。

そこで、もう一度、3つのオシレータのチャートを見てみましょう：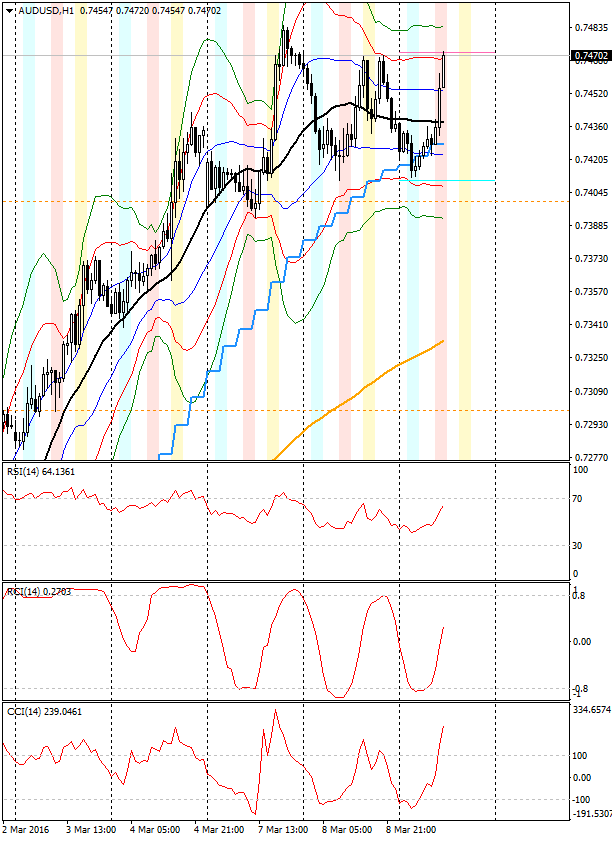



一番下の段がCCIです。

その真ん中あたり、CCIの値が急騰しているところでは、プライスがBB+3σを上に突き抜けていますね。

実際、CCIは300近くまで上がっていますから、BB+4σも超えていることがわかります。

このようにCCIはトレンドの勢いを見ることができる指標です。

特に、CCIが±100より外側にある状態というのは、プライスがBB±1.5σの外側で推移していることを表しており、BB±\(\sqrt{3}\)σがトレンドの分水嶺であることを考え合わせると、トレンドが出現していることを直感的に示す指標だと言うことができます。

なので、CCIは一見オシレータのように見えますが、実はトレンド系の指標だと考えることができます。


もっと言えば・・・


オシレータとトレンド系指標というのは、見方によって変わってくるものなのです。


その最たる実例は、「学習プログラム（三種の原理）」でメンバーの方にご提供している、あのマイクのオリジナル・インジケータです。

この話は始めると長くなるので、またの機会にじっくり解説したいと思います。

どうぞお楽しみに♪


では、今日もポチっと応援お願いします☆

↓↓↓↓↓↓