こんにちは、マイクです。

今日は朝からテニスのシングルス大会に参加しました。

2ブロックのリーグ戦後、それぞれのリーグ1位の2人で決勝戦というシステムでした。

マイクはリーグ戦3勝1敗で同率1位でしたが、ゲーム獲得率が21/34、もう一人(某テニススクールのコーチ)が22/35で、
\[\frac{22}{35}-\frac{21}{34}=0.01\]
の僅差で惜しくも決勝進出を逃しました。

でも、たっぷり楽しめてよかったです♪


さて今日は、通貨ペアや時間足に依存せず、その時のトレンドの勢いを統一的に表現できるように、「MAの角度」を再定義してみたいと思います。


前回までの記事の復習はこちらから：

■「マイクの定理」とその応用(1)
■「マイクの定理」とその応用(2)
■「マイクの定理」とその応用(3)
■「マイクの定理」とその応用(4)
■「マイクの定理」とその応用(5)
■「マイクの定理」とその応用(6)
■「マイクの定理」とその応用(7)
■「マイクの定理」とその応用(8)


そもそも、「MAの角度」
\[A_n(t)=p(t)-p(t-n)\]
がなぜ通貨ペアや時間足に依存するかというと、生のプライスの差分で定義されているからです。


では、現在レートで基準化して、「変化率」の形にすればよいでしょうか？

この場合、通貨ペアによる違いは平準化されますが、時間足による違いは依然残っています。

5分足と日足では、同じ本数のローソク足でも、変化率は全く違いますからね。

つまり、5分足と日足では、「ボラ」が全く違うということです。


だったら、その「ボラ」で基準化してあげましょう！

ボラを計る代表的指標と言えば・・・


そうです、ATR (Average True Range)です。


期間\(n\)の時刻\(t\)におけるATR \(R_n(t)\)は次式で定義されます：

\begin{align}R_n(t)=\frac{1}{n}\sum_{j=0}^{n-1}\max[\,&H(t-j)-L(t-j)\,,\, \\&H(t-j)-C(t-j-1)\,,\, \\\\&C(t-j-1)-L(t-j)\,]\end{align}

ここで、\(H(t)\)、\(L(t)\)、\(C(t)\)は、それぞれ時刻\(ｔ\)におけるローソク足の高値、安値、終値です。

ざっくり言えば、窓開けを考慮した各バーの高値安値の幅の\(n\)期間平均ですね。

つまりこのATRは、平均的に1本のバーがヒゲを含めてどのくらいの幅を持っているかを示している指標と言えます。

とても直感的でわかりやすいですね♪


このATRでMAの角度\(A\)を基準化することによって、下記の「基準化角度」\(\tilde{A}\)を定義します：
\[\tilde{A}_n(t)=\frac{A_n(t)}{nR_n(t)}\]

分母に\(n\)があるのは、\(A\)を定義した時に横軸を期間\(n\)で基準化したので(以前の記事を参照)、それに揃えるためです。


では、前回の記事で比較した2つのチャートに、この基準化角度を表示させてみましょう：


【1】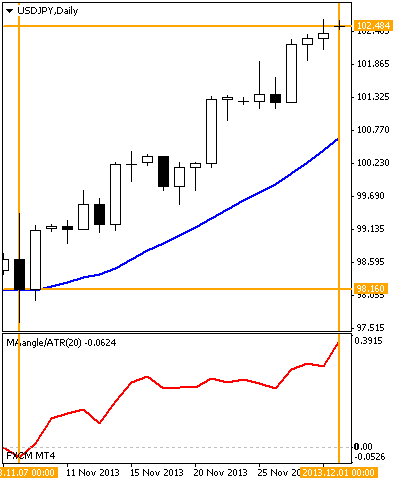

【2】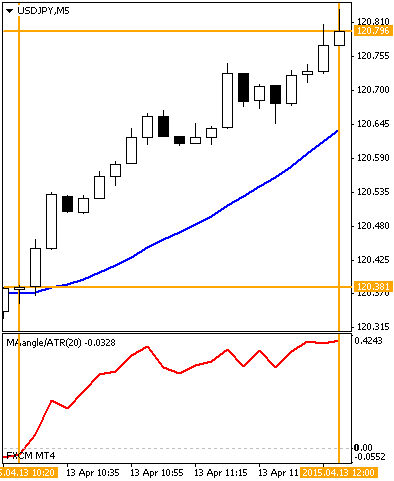



チャート下側のサブウィンドウが、基準化角度を表示するマイクのオリジナルインジケータです。

チャート右端における基準化角度の値は、

【1】 0.37
【2】 0.40

で、両方とも約0.4となっています(サブウィンドウの縦軸を見てください)。

【1】は日足、【2】は5分足ですが、基準化角度は時間足に依らずMAの角度を統一的な基準で表せることがわかります。

もちろん、ボラの異なる他の通貨ペアでも同じように統一的な評価が可能です。


そして、この基準化角度の値は、単に相対的なものではなく、ある重要な数理的性質を持っています。

これについては、次回詳しく解説しますね♪


では、今日もニャンコをポチっと☆