こんにちは、マイクです。
前回の記事に読者さんから嬉しいコメントを頂きました。
一部抜粋すると:
私も以前MAの角度を数値化(データ化)したいと思った事がありましたが、あまり深く考えず面倒臭そうだと諦めていました。。
そんな中、「マイクの定理」とその応用(8) と 「マイクの定理」とその応用(9)は目から鱗が落ちるようでした!
私の知る限りMAの角度を基準化、比較する方法をネット上でこれ以上に分かり易く解説してるサイトは見つかりません。
本当にありがとうございますm(_ _)m
こちらこそ記事を高く評価して頂き、ありがとうございます!
こういうコメントを頂くと、記事を書いてよかったな~と思いますね♪
では、今回は「基準化角度」の持つ重要な数理的性質についてです。
前回までの記事の復習はこちらから:
■「マイクの定理」とその応用(1)
■「マイクの定理」とその応用(2)
■「マイクの定理」とその応用(3)
■「マイクの定理」とその応用(4)
■「マイクの定理」とその応用(5)
■「マイクの定理」とその応用(6)
■「マイクの定理」とその応用(7)
■「マイクの定理」とその応用(8)
■「マイクの定理」とその応用(9)
まず、前回示したチャートをもう一度ご覧ください:
【1】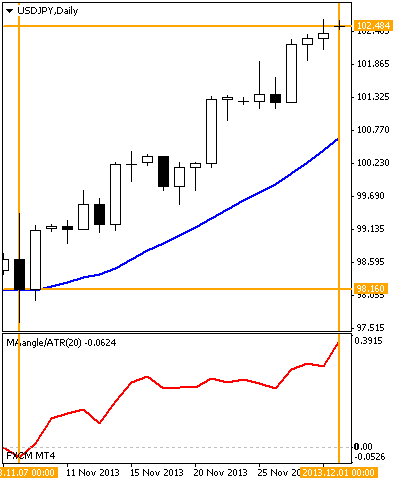
【2】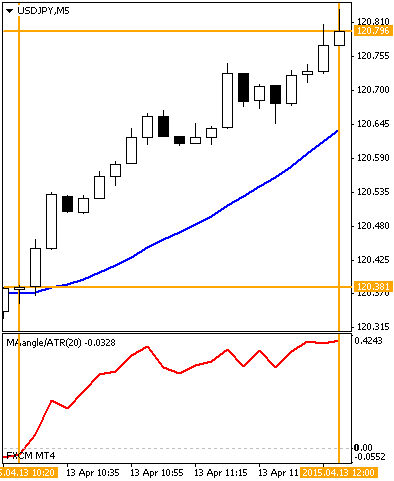
チャート右端における基準化角度の値は、【1】【2】とも約0.4でしたね。
では・・・
この値は最大いくつまで大きくなり得るでしょうか?
どう思いますか?
考えましたか?
答は:
基準化角度の絶対値は1以下であり、1となるのは○○○○○の場合である。
そうなんです!
基準化角度は相場がどのように動いても大きさが1を超えることはありません。
つまり、基準化角度は「最も急な角度」に対する比でもあるわけです。
「基準化」という言葉が伊達ではないことがわかりますね♪
では・・・
1となる○○○○○の場合って、どんな場合でしょう?
これは次回までの宿題としましょうね。笑
みなさん、考えてみてください。
では、今日もニャンコをポチっと☆

ヨスケです。
マイクさん、昨日のコメントへの返信ありがとうございますm(_ _)m
覚えて頂けてて光栄です!またマイクさんとお話したいです(*´∀`*)
折角の宿題なので回答させて頂きます。
基準化角度が1となるのは、ズバリ 『MAが水平』 の場合ではないでしょうか?
仮にローソク足の終値を使った20MAの場合でしたら、
現在レートと、20本前のローソク足の終値レートが”同じ”状態だと思います。
明日の記事も楽しみにしてま~す!
ヨスケさん、こんばんは。
宿題への回答ありがとうございます!
アウトプットする姿勢、素晴らしいですね。
さて、おっしゃるように、「MAが水平の場合、現在レートと、20本前のローソク足の終値レートが同じ(20MAの場合)」であるのはその通りです。
でも、そしたら、マイクの定理によって、MAの角度は0になりますよね?
直感的に考えても、MAが右上がりなら正(+)、右下がりなら負(-)ですから、水平だったら0ですね。(^^)
±1になるのは「最強に」上昇(下降)している時です。
さてそれは具体的には?
次の記事までにもう少し考えてみてください♪
マイクさん、こんにちは(*´∀`*)
ヨスケです。
返信ありがとうございます!
恥ずかしい間違いをしました(^_^;)
確かに下向きがマイナスになる事を考えれば
水平は0というのは理解し易いですね!
最強に上昇してる基準化角度が1の状態…
「ATR×20」の値と「現在レート – 20本前ローソク足終値」が同じ場合でしょうか?
最新のレートが20期間の内、最高値。
20本前のローソク足が期間中の終値ベースで最安値。
であるだけでなく、その20本のローソク足にヒゲが一切無く全て陽線という状態だと思います。
期間中にヒゲが少しでもでてしまうと
ATR×20 > 現在レート – 20本前ローソク足終値
に必ずなってしまうと思いますので。
説明が分かり難いかもしれませんが、改めて回答とさせて頂きますm(_ _)m
マイクさん、こんばんは♪
最近ストレートネックに悩んでる、けだま。です。
基準化角度のは、背筋ピーン!(垂直)ですかね?
MAは垂直になれませんが、
自分はMANなので基準化角度1になれるよう頑張ります…!!
(すみません、何を言ってるのかわからなくなりまs…
0度で0、90度で1、ふと、三角関数のsineを思い出しました…。
ヨスケさん、こんばんは!
次の記事でも書きましたが、大正解です!
ATRの性質をよく理解されてますね。
素晴らしいです♪
けだま。さん、こんばんは。
大爆笑してしまいました!(≧∇≦)
そう、MAは垂直にはなれませんね。
ただ、ステップ状になった場合はそれに近いです。
次の記事を見てみてくださいね♪