こんにちは、マイクです。
前回の記事で出した宿題、みなさん考えましたか?
基準化角度の絶対値は1以下であり、1となるのは○○○○○の場合である。
○○○○○の場合ってどんな場合??
という質問でしたね。
この宿題に、読者さんから幾つも回答を頂きました!
アウトプットする姿勢、素晴らしいですね♪
あ、前回までの記事の復習はこちらから:
■「マイクの定理」とその応用(1)
■「マイクの定理」とその応用(2)
■「マイクの定理」とその応用(3)
■「マイクの定理」とその応用(4)
■「マイクの定理」とその応用(5)
■「マイクの定理」とその応用(6)
■「マイクの定理」とその応用(7)
■「マイクの定理」とその応用(8)
■「マイクの定理」とその応用(9)
■「マイクの定理」とその応用(10)
で、その回答の中に、バッチリ大正解がありましたよ!
それは、ヨスケさんの回答です:
「ATR×20」の値と「現在レート – 20本前ローソク足終値」が同じ場合でしょうか?
最新のレートが20期間の内、最高値。
20本前のローソク足が期間中の終値ベースで最安値。
であるだけでなく、その20本のローソク足にヒゲが一切無く全て陽線という状態だと思います。
期間中にヒゲが少しでもでてしまうと
ATR×20 > 現在レート – 20本前ローソク足終値
に必ずなってしまうと思いますので。
「ヒゲが一切無く全て陽線」というところがポイントですね。
基準化角度の定義は
\[\tilde{A}_n(t)=\frac{A_n(t)}{nR_n(t)}=\frac{p(t)-p(t-n)}{nR_n(t)}\]
なので、それが1となる、つまり分子と分母が等しくなるのは、各ローソク足のヒゲを含めた幅を期間にわたって足したものが、その期間の両端でのプライスの差に等しくなる時ですから、ヨスケさんのおっしゃるように、ヒゲが少しでも出てしまうと、分母の方が大きくなって、基準化角度の大きさは1より小さくなってしまうわけです。
指標の意味をよく理解していないとわからないことだと思いますので、ヨスケさん、素晴らしいですね♪
細かい話をすると、窓開けがある場合には、ラップしない範囲でヒゲがあっても大丈夫ですが、ここでは前の足の終値と次の足の始値が同じという一般的な条件で話を進めます。
では、ほんとに丸坊主の陽線(陰線)が続く時±1になるのか、確かめてみましょう!
■丸坊主の陽線が続く場合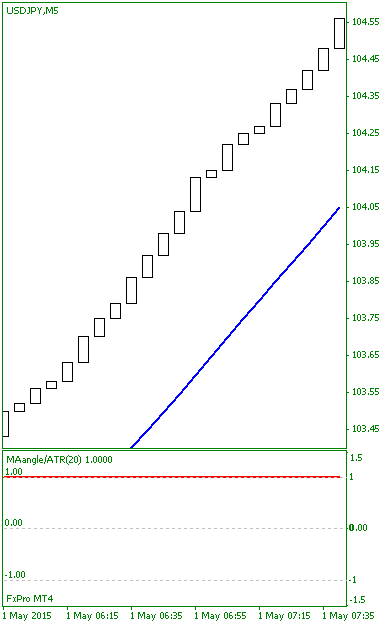
■丸坊主の陰線が続く場合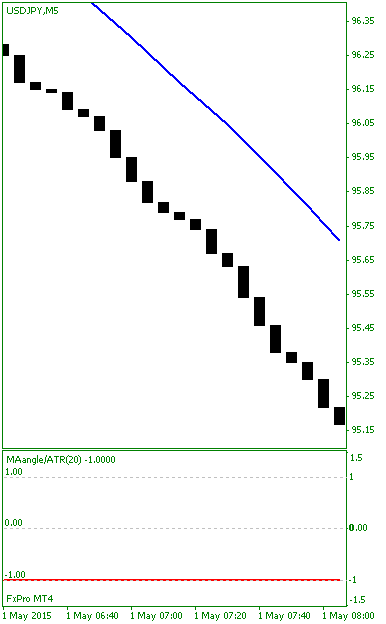
おー、確かに、
丸坊主の陽線が続く時は\(+1\)に、
丸坊主の陰線が続く時は\(-1\)に、
べったり張り付いてますね!
丸坊主の陽線や陰線が続くということは、まったく押し戻しをつけずに、一方的にプライスが進み続ける状態です。
まさに「最強の」トレンドと言えますね。
この状態の時にのみ基準化角度の大きさは最大値である1となるわけです。
基準化角度がトレンドを計る指標として、非常に直感的かつ合理的に設計されていることがわかるかと思います。
マイクはいつもこの基準化角度の値を見てトレンドの勢いを評価しています。
具体的な判断方法はまた別の機会にお伝えできればと思います。
さて、気が付けば11回(!)にわたりお届けしてきた
「マイクの定理」とその応用
ですが(こんなに長くなるとは思わなかった・笑)、今回で一段落とします。
そして、明日は重要なお知らせがありますので、見逃さないでくださいね♪
では、今日もニャンコをポチっと☆
