こんにちは、マイクです。

前回の記事では、移動平均をデジタルフィルタとして捉え、SMAの周波数特性を計算しました。

今日はその周波数特性が示すSMAの特徴について見ていきましょう。

SMA(期間20)の周波数特性を再掲します：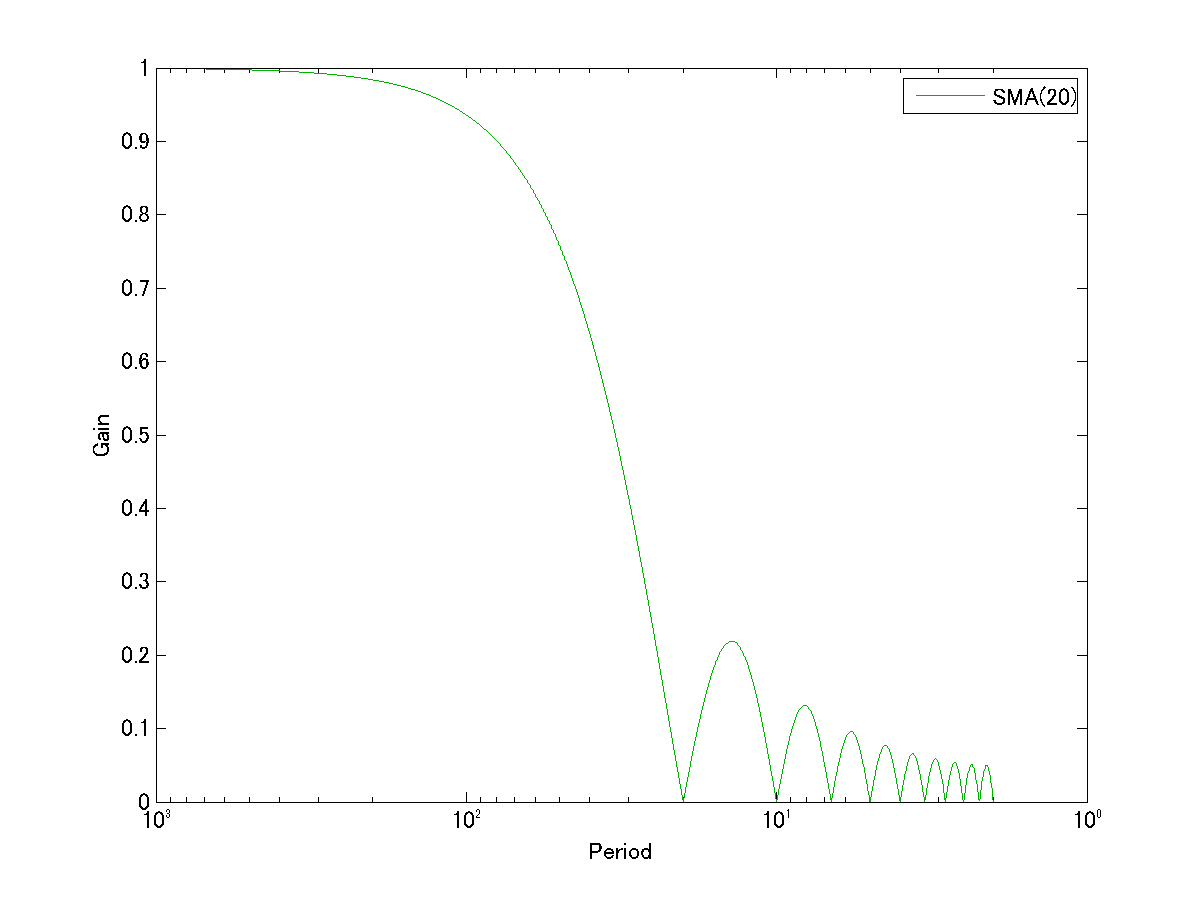


横軸は周期ですが、普通の横軸とは逆に右に行くほど小さくなっています。

周波数特性は通常、横軸を周波数\(f\)(周期\(T\)の逆数)で表現するので、それに合わせたわけですね。

つまり、横軸の左の方が低い周波数(長い周期)、右の方が高い周波数(短い周期)に対応しています。


まずこのグラフを見ると、SMAの最も重要な特徴が明確に示されています。

グラフの曲線は、大まかに言うと、低周波(長周期)ではほぼ1で、高周波(短周期)になるにつれて小さくなっています。

これは、SMAがローパスフィルタ(low-pass filter)の特性を有していることを示しています。

ローパスフィルタは高周波のノイズをカットするために使われるフィルタです。

SMAを表示することによって、ヒゲを含めたローソク足1本ずつの細かい動きが平滑化され、より長い周期の変動が見やすくなることと、見事に対応していますね！


そして、もう一つSMAの周波数特性で特徴的なのは、\(T\)=20の点を始めとして、曲線の大きさが0になっている点が何点かあるということです。

具体的に挙げると、\(T\)=20, 10, 6.7, 5, 4, 3.3, 2.9, 2.5, 2.2, 2の各点です。

これを見て以前の記事を思い出した方は鋭いですね！

そうです。

上記の各周期は、その整数倍がSMAの期間20になる点です。

値動きがこのような周期を持つ時、SMAはどうなるのでしたっけ？

・・・

完全に水平になるのでしたね。

つまり、周波数特性が0なので、全く動かなくなるわけです！


周波数特性を見るだけで、これらのSMAが持つ特徴が一目でわかってしまいます♪

すごいですね！


では、次回はEMAの周波数特性を見てみましょう。


あ、その前に・・・

前回の記事で、デジタルフィルタにはFIRとIIRの2種類があると言いましたが、EMAはどちらになるでしょうか？

次回までに考えておいてくださいね♪


では、今日もポチっと応援お願いします☆

↓↓↓↓↓↓