こんにちは、マイクです。

先週末の米国雇用統計は、市場予想を若干上回る結果でした。

これで今月の利上げは完全に織り込まれたと考えられます。

既に市場の関心は、来年の利上げペースがどうなるかに移っているようですね。


さて、MAの話も早いもので10回目となりました。

そして、タイトルにもあるように、この記事は実は猫カフェで書いています。

かわいいニャンコ達がたくさん徘徊していて、めちゃ癒されています。笑


こんなのとか：



カフェラテも猫♪：




うーん、たまらんにゃ


さて、前回の記事では、SMAの周波数特性とそれが表すSMAの特徴について見てきました。

今回はEMAの周波数特性を見てみましょう。


その前に・・・

前回のクイズの答は考えましたか？

• デジタルフィルタにはFIRとIIRの2種類があると言いましたが、EMAはどちらになるでしょうか？

というものでした。


勘のいい方は第２回で示したEMAの定義式を思い出したかもしれませんね：


\[\mathrm{EMA}(t)=\alpha\sum_{j=0}^{\infty}(1-\alpha)^j p(t-j)\tag{1}\]


ここで平均を取る項が無限大(\(\infty\))までになっていることに気付けば、EMAがIIRフィルタであることがわかったかと思います。


では、具体的にフィルタの多項式\(A\), \(B\)はどうなっているのでしょうか？

それは、第４回で示したEMAの計算方法からわかります：

\[\mathrm{EMA}(t)=\alpha p(t)+(1-\alpha)\mathrm{EMA}(t-1)\tag{2}\]


これを、第８回で示したデジタルフィルタの入出力関係

\[A(z)y(t)=B(z)u(t)\tag{3}\]

に従って表すと、

\[(1-(1-\alpha)z^{-1})y(t)=\alpha u(t)\tag{4}\]

と書けるので、結局、

\[A(z)=1-(1-\alpha)z^{-1}\tag{5}\]

\[B(z)=\alpha\tag{6}\]

であることがわかります。


よって、伝達関数は

\[H(z)=\frac{B(z)}{A(z)}=\frac{\alpha}{1-(1-\alpha)z^{-1}}\tag{7}\]

となります。

これに

\[z=e^{i\omega}\tag{8}\]

を代入すると、

\[H(\omega)=\frac{\alpha}{1-(1-\alpha)e^{-i\omega}}\tag{9}\]

という周波数特性が得られました！


EMAの期間が20の場合について図示するとこうなります：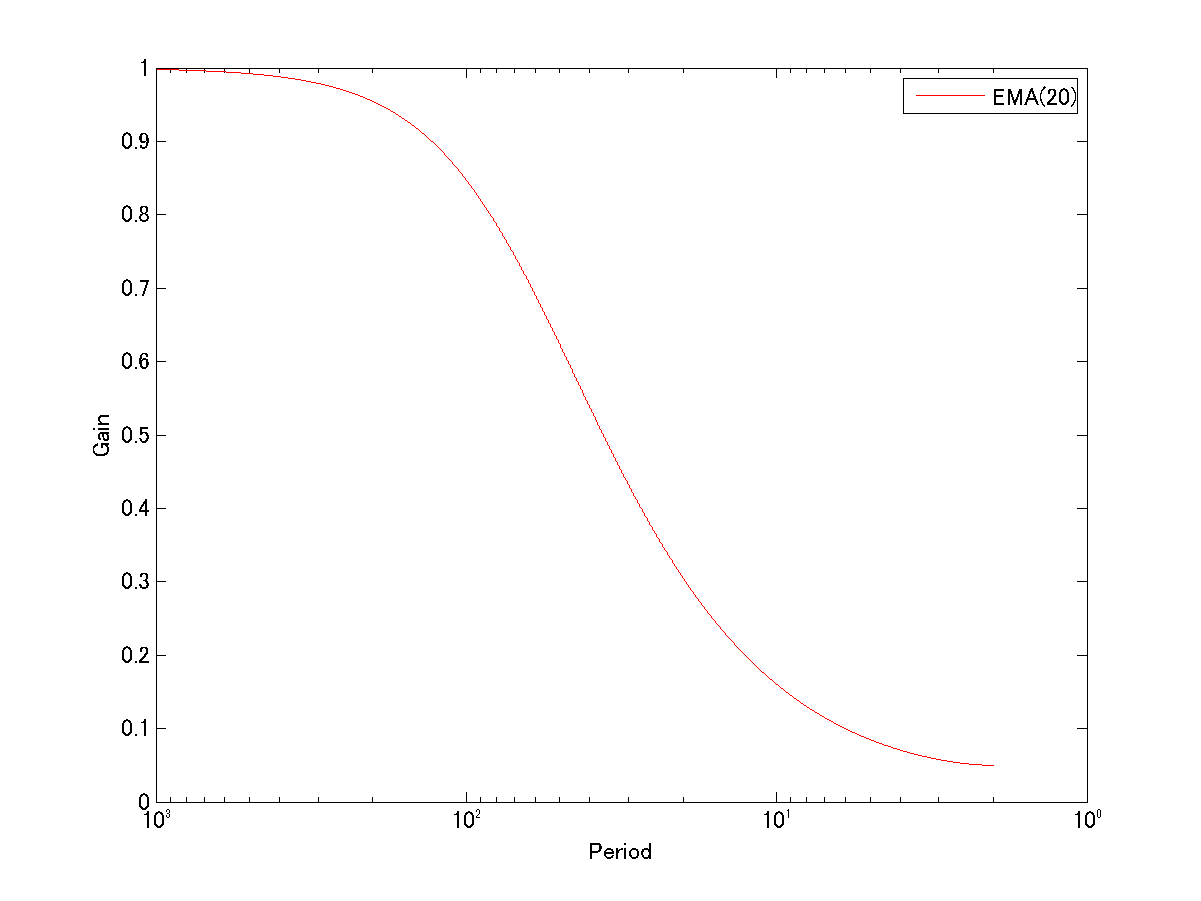



SMAと一緒に表示すると：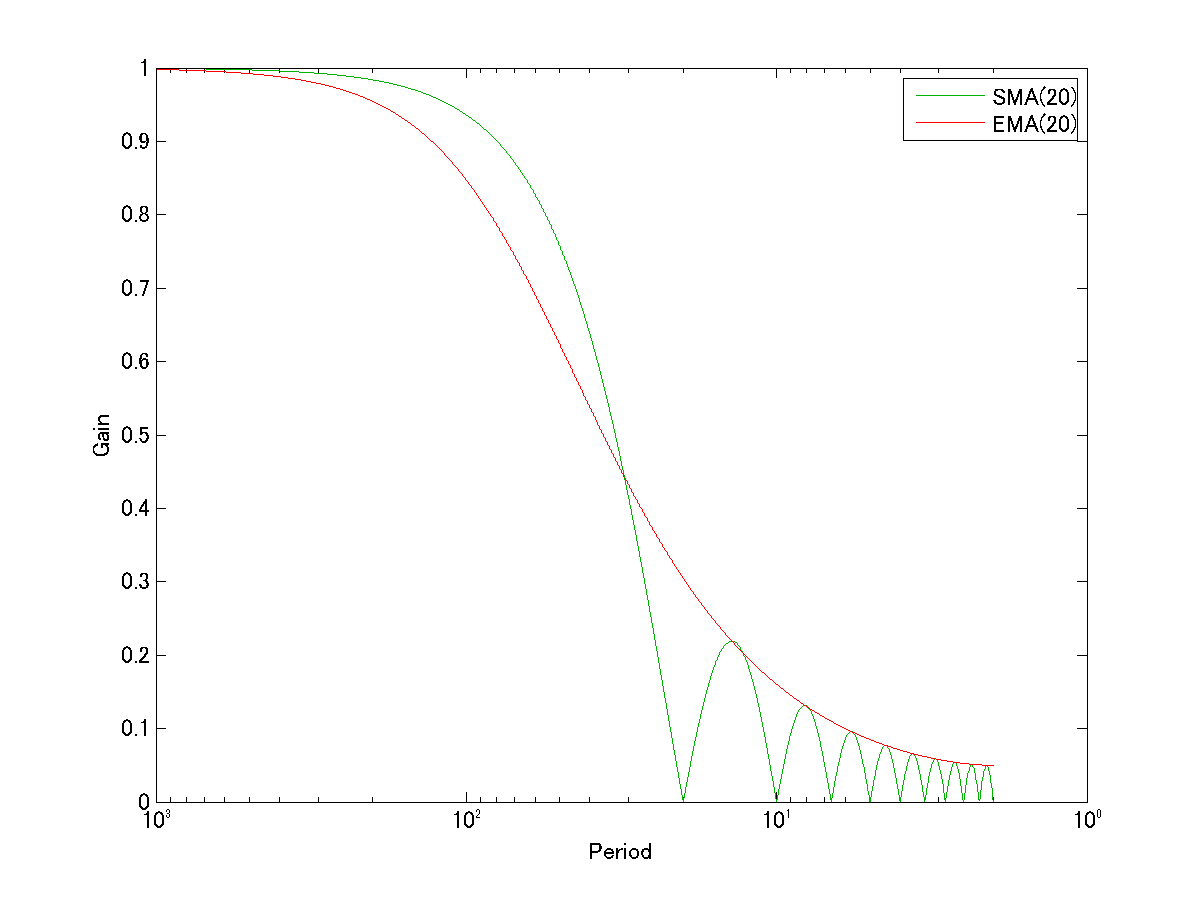


となります。

この図が示すEMAの特徴については、また次回にしましょう♪


では、今日もポチっと応援お願いします☆

↓↓↓↓↓↓