こんにちは、マイクです。
前回の記事では、EMAの周波数特性を計算し、SMAと比較して図示しましたね。
今回は、その周波数特性が表すEMAの特徴について考察します。
■知っているようで知らないMAの話(1:SMAとEMAの違い)
■知っているようで知らないMAの話(2:EMAの「期間」って何?)
■知っているようで知らないMAの話(3:SMAとEMAの重みの関係は?)
■知っているようで知らないMAの話(4:EMAの実際の計算方法)
■知っているようで知らないMAの話(5:EMAの角度とローソク足の位置との関係)
■知っているようで知らないMAの話(6:正弦波状の値動きに対するSMAとEMA)
■知っているようで知らないMAの話(7:急変した値動きに対するSMAとEMA)
■知っているようで知らないMAの話(8:デジタルフィルタとしての移動平均)
■知っているようで知らないMAの話(9:SMAの周波数特性)
■知っているようで知らないMAの話(10:猫カフェよりお届けします)
本題に行く前に・・・
前回の記事のニャンコが大好評で、他のニャンコも~!というリクエストをもらいましたので:
いや~、かわいいですね!![]()
また訪れた時にはアップしますので、お楽しみに♪
では本題に。笑
周波数特性の図を再掲します: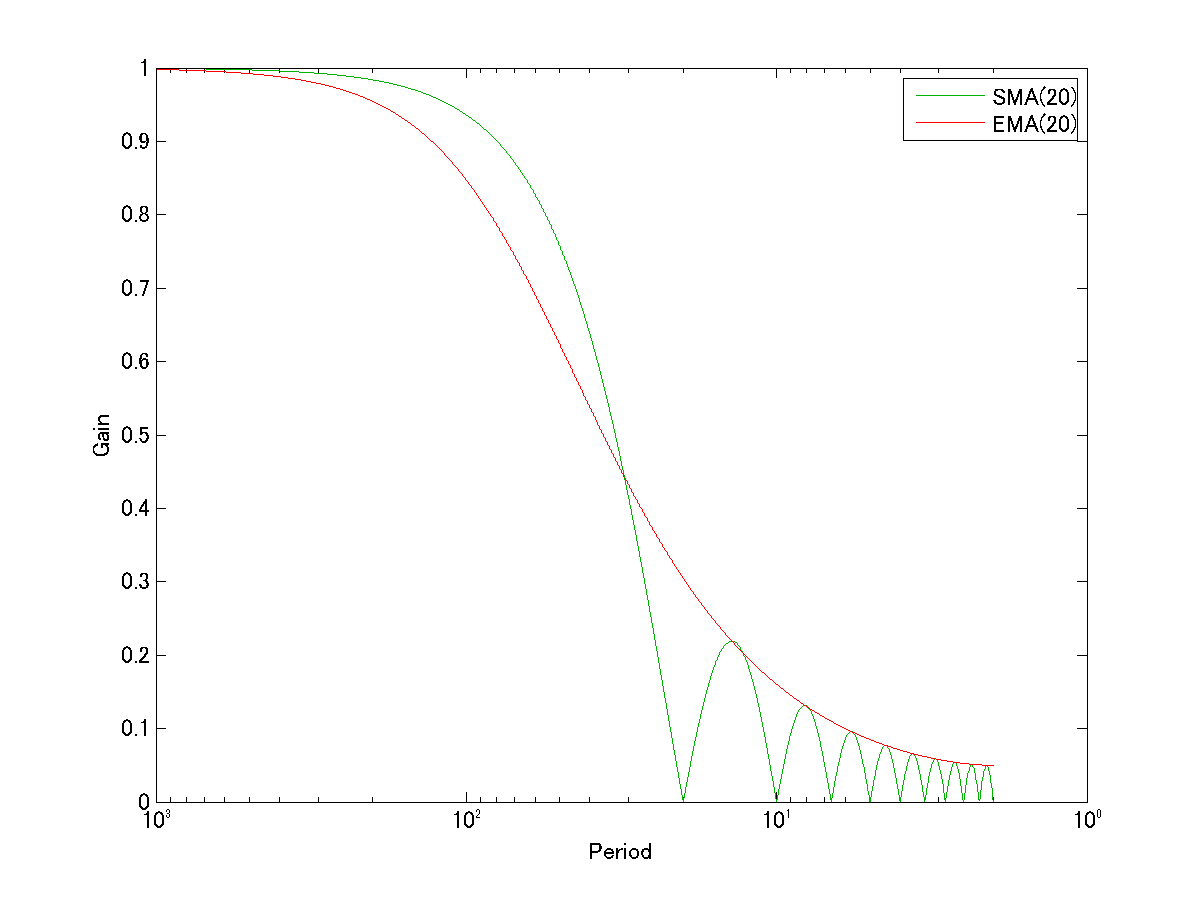
緑が前出のSMAの周波数特性、そして、赤がEMAの周波数特性です。
ここからは、EMAの特徴として、主に3つのことが読み取れます。
まず第1に、SMAと同様にEMAもローパスフィルタの特性を持っているということです。
つまり、短い周期の変動をカットして、より長い周期の変動を見やすくする効果があるということですね。
第2には、SMAで見られたような、ゲインが0になる点が存在しないというみことが挙げられます。
第6回で見たように、MAの期間と同じ周期の値動きがあった時、SMAの場合には完全に水平になりますが、EMAはその周期で変動します。
周波数特性を見ると、プライスが一定でない限り、どんな周期の値動きに対しても、EMAが水平のままで推移することはないことがわかります。
そして第3に、周期の長い範囲ではSMAの方がゲインが大きく、逆に周期の短い範囲ではEMAの方がゲインが大きいことがわかります。
つまり、EMAの方がSMAより落ちてくる勾配がなだらかですね。
なので、ある程度短い周期の変動もEMAには反映されることになります。
これが、同期間のEMAの方がSMAよりもローソク足への追従性がよい理由となっています。
さて、11回にわたってMAの話をお送りしてきましたが、とりあえず今回で〆ましょう(飽きてきたという説も・笑)。
連載によって、この一番身近なインジケータに対する理解と愛着が深まっていれば幸いです♪
では、今日もポチっと応援お願いします☆
